Completing with the so called slack variables #s_1,s_2# we propose an equivalent problem to be handled with the Lagrangian Multipliers technique.
Minimize/maximize
#f(x,y)=(e^(yx)-e^(-yx))/(2yx)#
subjected to
#g_1(x,y,s_1) = x^2/y+y^2/x-s_1^2-1=0#
#g_2(x,y,s_2) = x^2/y+y^2/x-s_2^2-3=0#
The lagrangian reads
#L(x,y,s_1,s_2,lambda_1,lambda_2)=f(x,y)+lambda_1g_1(x,y,s_1)+lambda_2 g_2(x.y,s_2)#
The lagrangian stationary points includes the local maxima/minima points.
The stationary points are the solutions of
#grad L(x,y,s_1,s_2,lambda_1,lambda_2)=vec 0#
or
#{
((e^(-x y) y + e^(x y) y)/(2 x y) -(-e^(-x y) + e^(x y))/(2 x^2 y) + lambda_1 ((2 x)/y - y^2/x^2) + lambda_2 ((2 x)/y - y^2/x^2) = 0),
( (e^(-x y) x + e^(x y) x)/(
2 x y) -(-e^(-x y) + e^(x y))/(2 x y^2) + lambda_1 ((2 y)/x-x^2/y^2) + lambda_2 ( (2 y)/x-x^2/y^2) =
0),
(-1 - s_1^2 + x^2/y + y^2/x = 0),
(-2 lambda_1 s_1 = 0),
(-3 + s_2^2 + x^2/y + y^2/x = 0),
(2 lambda_2 s_2 = 0)
:}#
Solving for #x,y,s_1,s_2,lambda_1,lambda_2# with an iterative procedure such as Newton-Raphson's we obtain
#(
(x = 1.5, y = 1.5, lambda_1 = 0, s_1=-1.41421, lambda_2 = -1.80774,
s_2 = 0),
(x= 1.5, y = 1.5, lambda_1 = 0, s_1 = 1.41421, lambda_2= -1.80774, s_2 = 0),
(x = 0.5, y = 0.5, lambda_1 = -0.0419277, s_1 = 0, lambda_2 = 0,
s2 = -1.41421),
(x = 0.5, y=0.5, lambda_1= -0.0419277, s_1= 0, lambda_2= 0,
s_2= 1.41421)
)#
There are four solutions but for two points. The first #{1.5,1.5}# activates #g_2(x,y,0)# and the second #{0.5,0.5}# activates #g_1(x,y,0)# so their qualification must be against
#f@g_1 =((2/3)^(1/3) x)/(-9 x^3 + sqrt[3] sqrt[-4 x^3 + 27 x^6])^(
1/3) + (-9 x^3 + sqrt[3] sqrt[-4 x^3 + 27 x^6])^(1/3)/(
2^(1/3) 3^(2/3))#
and
#f@g_2=(3 2^(1/3) x)/(-x^3 + sqrt[-108 x^3 + x^6])^(
1/3) + (-x^3 + sqrt[-108 x^3 + x^6])^(1/3)/2^(1/3)#
Calculating
#(d^2)/(dx^2)f@g_1(0.5,0.5)=-1.5094# local maximum
#(d^2)/(dx^2)f@g_2(1.5,1.5)=-21.6928# local maximum
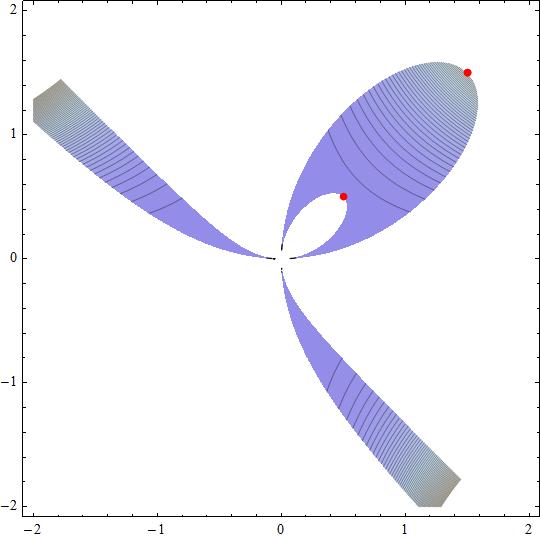
Attached the figure with the feasible region showing the #f(x,y)# contour map and the local extrema points.