Question

A ball with a mass of `5` `kg` is rolling at `4` `ms^-1` and elastically collides with a resting ball with a mass of `3` `kg`. What are the post-collision velocities of the balls?

Answer 1

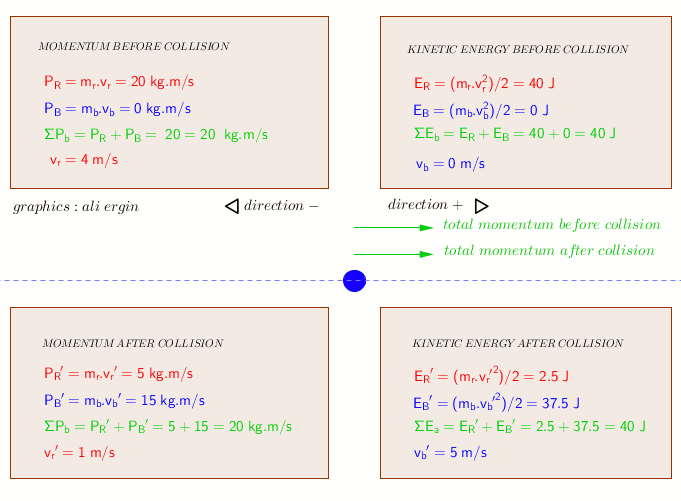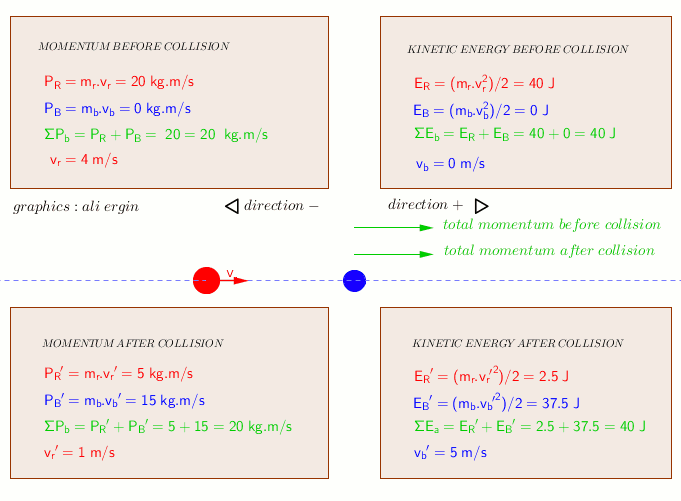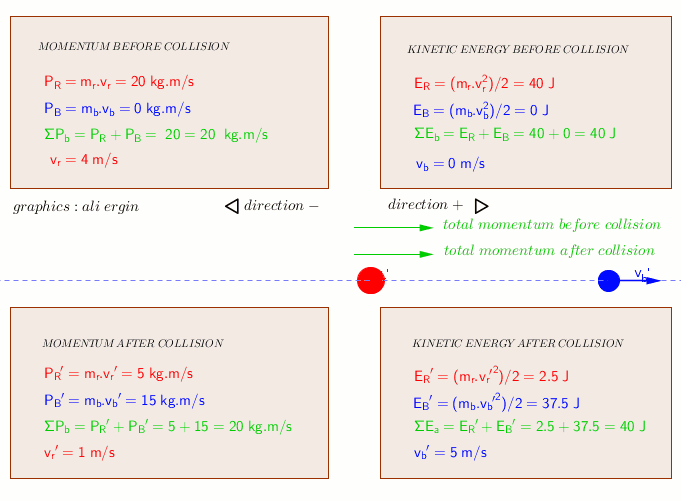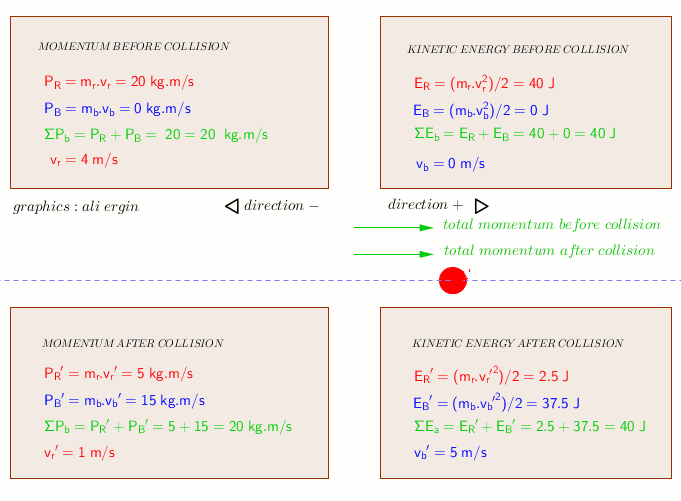
Momentum is always conserved, and the key word 'elastically' tells us that kinetic energy is also conserved. The calculation below shows how we determine the final velocities of the balls, which are `v_1=3.88` `ms^-1` and `v_2=0.12` `ms^-1`.

Explanation:

Momentum before the collision: `p=mv=5*4=20` `kgms^-1`

Kinetic energy before the collision: `E_k=1/2mv^2=1/2xx5xx4^2=40` `J`

(the stationary ball has a momentum of `0` `kgms^-1` and a kinetic energy of `0` `J` before the collision)

The fact that momentum and kinetic energy are conserved mean that the total momentum after the collision will be `20` `kgms^-1` and the total kinetic energy after the collision will be `40` `J`.

Call the `5` `kg` ball '1' and the `3` `kg` ball '2'.

For momentum:

`m_1v_1+m_2v_2=20` - call this equation (A)

For kinetic energy:

`1/2m_1v_1^2+1/2m_2v_2^2=40` - call this equation (B)

We can substitute in the known masses to make these simpler:

`5v_1+3v_2=20` - (A')

`5/2v_1^2+3/2v_2^2=40` - (B')

To make it even a little neater, let's multiply equation B' by 2:

`5v_1^2+3v_2^2=80` - (B'')

Rearranging equation A', `v_1=4-3/5v_2`

Substituting this value of `v_1` into B'':

`5(4-3/5v_2)^2+3v_2^2=80`

Expanding the square:

`5(16-24/5v_2+9/25v_2^2)+3v_2^2=80`

`80-24v_2+9/5v_2^2+3v_2^2=80`

Subtract 80 from both sides and rearrange:

`24/5v_2^2=24v_2`

Multiplying through by 5 (I hate fractions):

`24v_2^2=120v_2`

Dividing through by `v_2`:

`24v_2=120`

`v_2=0.2` `ms^-1`

Substituting back into A':

`v_1=4-3/5(0.2)=3.88` `ms^-1`

We can substitute these values back into A and B to check them.

Answer 2

`"please look over the animation for details"`
`v_r^'=1 " "m/s`
`v_b^'=5" " m/s`

Explanation:

`"solution-1:"`
`m_r:"the red ball's mass"`
`m_b:"the blue ball's mass"`
`v_r:"the velocity of red ball before collision"`
`v_b:"the velocity of blue ball before collision"`
`v_r^':"the velocity of red ball after collision"`
`v_b^':"the velocity of blue ball after collision"`

`"momentums before collision"`
`P_r=m_r*v_r=5*4=20 kg*m/s" the red ball's momentum"`
`P_b=m_b*v_b=3*0=0" the blue ball's momentum"`
`Sigma P=P_r+P_b=20+0=20 kg*m/s" thee total momentum"`

`v_r^'=(2*Sigma P)/(m_r+m_b)-v_r`

`v_r^'=(2*20)/(5+3)-4`

`v_r^'=40/8-4`

`v_r^'=5-4=1" " m/s`

`v_b^'=(2*Sigma P)/(m_r+m_b)-v_b`

`v_b^'=(2*20)/(5+3)-0`

`v_b^'=40/8-0`

`v_b^'=5" "m/s`

`"Solution -2:"`

`m_r*v_r+m_b*v_b=m_r*v_r^'+m_b*v_b^'`

`5*4+3*0=5*v_r^'+3*v_b^'`

`20=5*v_r^'+3*color(red)(v_b^')" (1)"`

`v_r+v_r^'=v_b+v_b^'`

`4+v_r^'=0+v_b^'`

`color(red)(v_b^')=4+v_r^'" (2)"`

`"(1) " 20=5*v_r^'+3*(4+v_r^')`

`20=5v_r^'+12+3v_r^'`

`20-12=8v_r^'`

`8=8v_r^'" ; "v_r^'=1" "m/s`

`"use (2)"`

`v_b^'=4+1=5" "m/s`