Question

Let R be the shaded region in the first quadrant enclosed by the y-axis and the graphs of `y=4-x^2` and `y=1+2sinx`, how do you find the volume of the solid whose base is R and whose cross sections perpendicular to the x-axis are squares?

Answer 1

`= int_(x=0)^(1.102) \ (3 - x^2 - 2 sin x)^2\ dx`

Explanation:

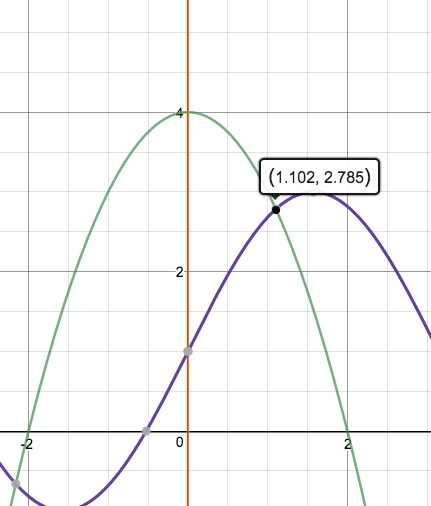
at any given x, the cross section area of the square will be

`A(x) = (y_2 - y_1)^2` {where `y_2` is the green line in the attached plot}

with `y_2 = 4 - x^2`

and `y_1 = 1 + 2 sin x`

so volume V(x) follows as

`V(x) = int_(x=0)^(1.102) \ A(x) \ dx`

`= int_(x=0)^(1.102) \ (3 - x^2 - 2 sin x)^2\ dx`

Please note that I got the 1.102 off the Desmos plot included here. I did not solve it myself.

Also that integral is horrendous so I would recommend a computer solution if you have access. This is really not something you want to be doing by hand.