How do you find the Maclaurin Series for f(x) = e^(3x)?
1 Answer
Explanation:
There are about two ways we can go about finding a Maclaurin series. However, in some cases it is much easier and less time-consuming to use some known Maclaurin series that have already been derived.
For this particular problem, I'll try to derive the Maclaurin series from scratch. Then, we'll compare it to a known Maclaurin series.
As you may already know, a Maclaurin series is a special case of a Taylor series centered at
We can express a Maclaurin series as an infinite sum:
As this infinite sum already suggests, we have to compute some derivatives. The more terms your Maclaurin series has, the better the approximation. For this problem, I will only compute four, which is enough to spot a pattern.
We can now substitute these
By simplifying the denominator on each term we get
We can simplify even further if we notice that
Alternatively, if we know that
We can simply replace
Also, we can check if this approximation looks alright by graphing both the polynomial with four terms, as well as
Graph of
graph{e^(3x) [-10, 10, -5, 5]}
Graph of
graph{1 + 3x + 9/2 x^2 + 9/2 x^3 + 27/8 x^4 [-10, 10, -5, 5]}
If we overlap them both on one graph, we can see that this infinite sum does, in fact, look alright to the first four terms.
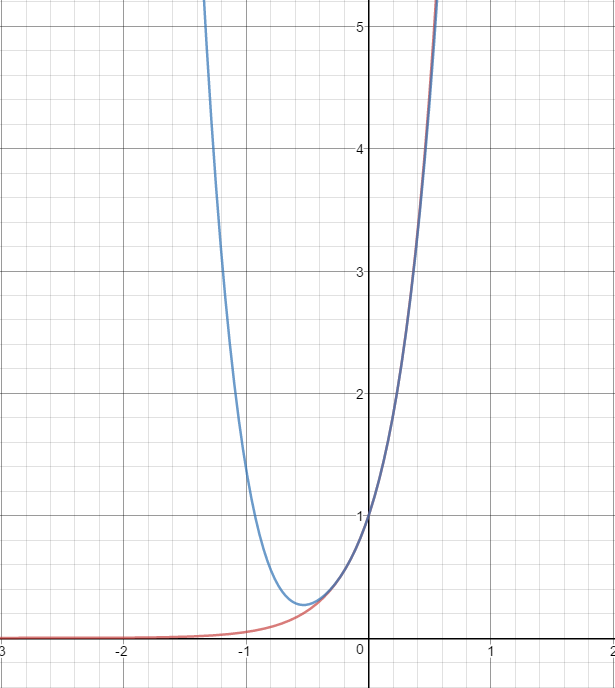
Red:
Blue:

