Question

How do you find the volume of the solid bounded by the coordinate planes and the plane `7x+y+z=4`?

Answer 1

`32/21`

Explanation:

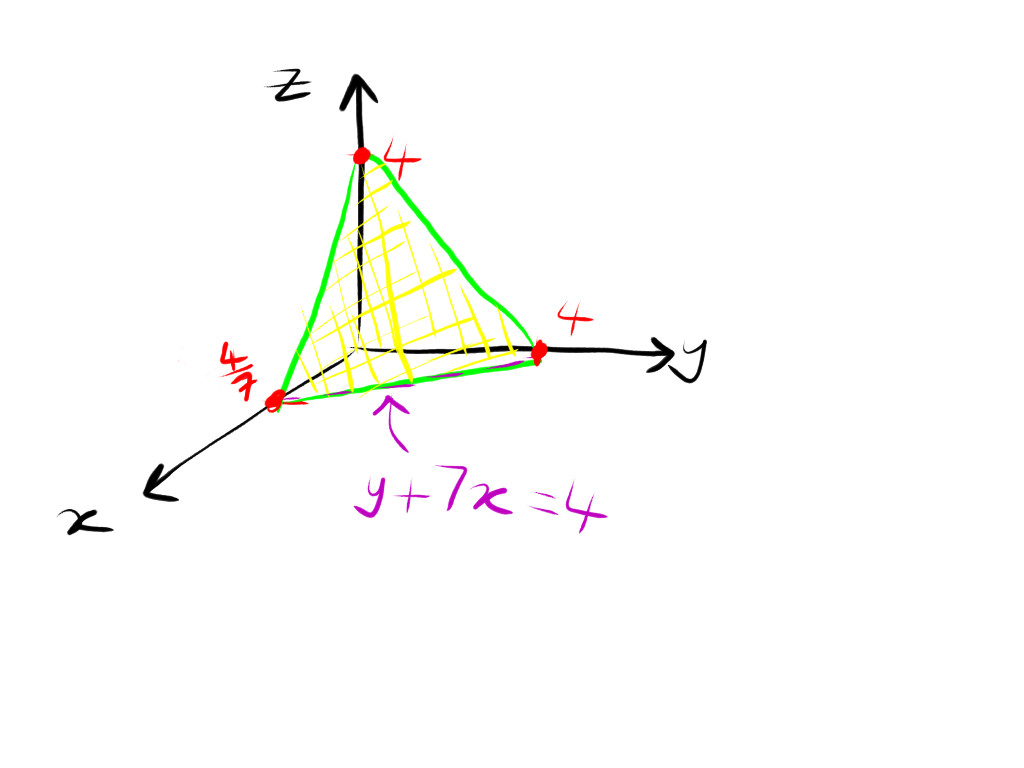
the drawing is key. start by finding the intercepts with each of the axes, the intercept line on the xy plane follows as `y + 7x = 4`

the volume is simply

`int int \ z(x,y) \ dA = int int \( 4 - 7x - y) \ dA`

it can be done as

`int_{y = 0}^{4} \ int_{x =0 }^{(4-y)/7} \ dx \ dy qquad ( 4 - 7x - y )`

OR

`int_{x = 0}^{4/7} \ int_{y =0 }^{4-7x} \ dy \ dx qquad ( 4 - 7x - y )`

in each case comes out at `32/21`