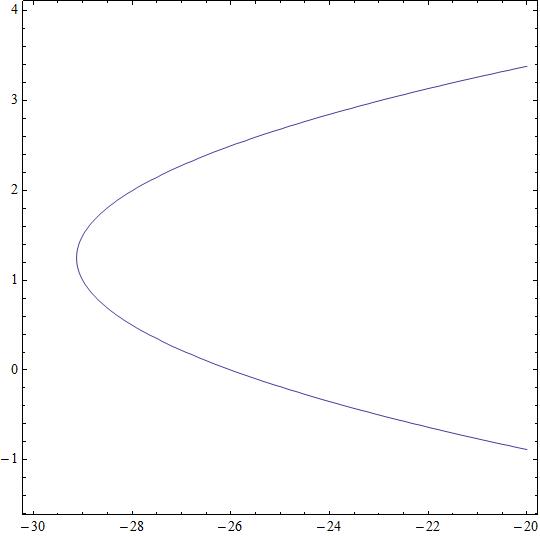
How do you classify the conic #-2y^2+x+5y+26=0#?

Question

1276 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-16T16:52:19

A parabola

Conics can be represented as

#p cdot M cdot p+<< p, {a,b}>>+c=0#

where #p = {x,y}# and

#M = ((m_{11},m_{12}),(m_{21}, m_{22}))#.

For conics #m_{12} = m_{21}# then #M# eigenvalues are always real because the matrix is symetric.

The characteristic polynomial is

#p(lambda)=lambda^2-(m_{11}+m_{22})lambda+det(M)#

Depending on their roots, the conic can be classified as

1) Equal --- circle
2) Same sign and different absolute values --- ellipse
3) Signs different --- hyperbole
4) One null root --- parabola

In the present case we have

#M = ((0,0),(0,-2))#

with characteristic polynomial

#lambda^2+2lambda=0#

with roots #{0,-2}# so we have a parabola.

Determining #{a,b,c}# is straightforward, solving the conditions for equating coefficients in

#-2 y^2 + x + 5 y + 26-(p cdot M cdot p+<< p , {a,b} >>+c) = 0 forall x in RR#

giving

#{a = 1, b = 5, c = 26}#

enter image source here