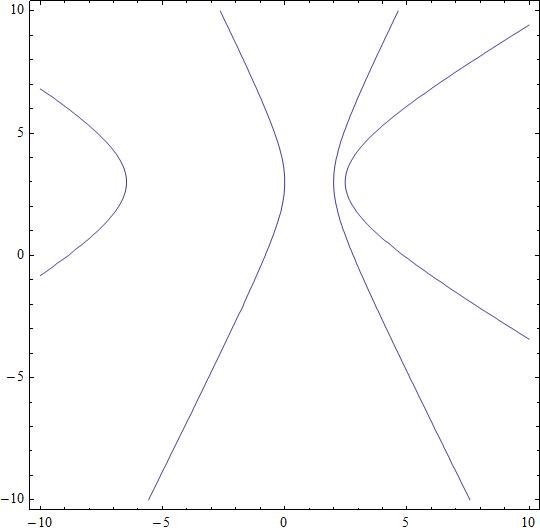
How do you solve the system #4x^2-y^2-8x+6y-9=0# and #2x^2-3y^2+4x+18y-43=0#?

Question

2533 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-25T17:28:38

No real solutions

Making #x^2=x_2# and #y^2=y_2# solve for #x_2,y_2# the system

# { (4 x_2 - y_2 - 8 x + 6 y - 9 =0), (x_2 - 3 y_2 + 4 x + 18 y - 43 = 0) :} #

resulting in

#{x_2 = 4/11 (7 x-4), y_2 = (24 x)/11 + 6 y-163/11}#

Now, solving for #x#

#x^2-28/11x+16/11=0# we obtain

#x = 2/11 (7 pm sqrt[5])#

Now, substituting #x# in

#y^2 = (24 x)/11 + 6 y-163/11#

and solving for #y# we cannot obtain real solutions.

Attached a graphic of the two conics.

enter image source here