Question

What is the distance between the following polar coordinates?: `(3,(-15pi)/12), (5,(-3pi)/8)`

Answer 1

`x = sqrt(3^2 + 5^2 - 2*3*5*cos({-15pi}/12 - {-3pi}/8)) ~~ 7.86`

Explanation:

Polar coordinates are written as `(r, theta)`, where `r` is the distance from the origin and `theta` is the angle with respect to the positive x-axis and the origin.

If we plot `(3, {-15pi}/12)` and `(5, {-3pi}/8)` on a graph, we notice we can form a triangle with the origin, `(0,0)`, as such:

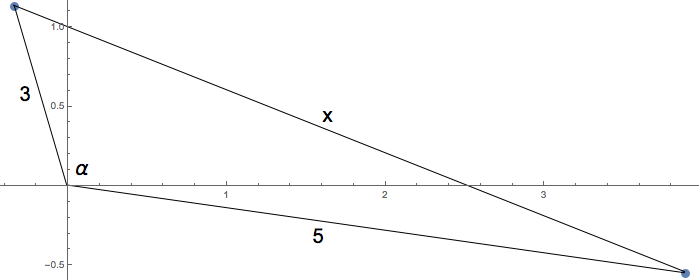
We know the length of two of the sides of the triangle, since the `r` value of the coordinates tell us. We can also calculate the angle `alpha`, since we have the angles of the two points.

`|theta_1 - theta_2| = |{-15pi}/12 - {-3pi}/8| = {7pi}/8`

If the result was larger than `pi`, we would simply subtract it from `2pi` to get the angle inside of the triangle.

Finally, we know from trigonometry that if we know two sides and the angle in between, we can calculate the length of the other side using the Law of Cosines:

`a^2 = b^2 + c^2 - 2bc cos(alpha)`

we can use this law to arrive at an equation for the distance between two polar points, `(r_1, theta_1)` and `(r_2, theta_2)`

`x = sqrt(r_1^2 + r_2^2 - 2r_1r_2cos(theta_1 - theta_2)`

or in this case,

`x = sqrt(3^2 + 5^2 - 2*3*5*cos({7pi}/8)) ~~ 7.86 square`

p.s. note the lack of absolute value signs in the final equation. That's because `cos(x) = cos(-x)`