Let #x=2sin(u) implies dx = 2cos(u)du#
#int (dx)/(x^2sqrt(4-x^2)) = int (2cos(u))/(4sin^2(u)sqrt(4 - 4sin^2(u)))du#
#= int (2cos(u))/(8sin^2(u)sqrt(1 - sin^2(u)))du#
#= int (2cos(u))/(8sin^2(u)sqrt(cos^2(u)))du#
#= int (2cos(u))/(8sin^2(u)cos(u))du#
#=1/4int (du)/(sin^2(u)) = 1/4int csc^2(u)du#
You can look up that the integral of #csc^2(x)# is equal to #-cot(x)# but we shall derive this anyway.
#int csc^2(x)dx = int (dx)/sin^2(x)#
Divide top and bottom by #cos^2(x)#
#int (sec^2(x))/(tan^2(x))dx#
Let #z = tan(x) implies dz = sec^2(x)dx#
#int (dz)/(z^2) = -1/z = -1/(tan(x)) = -cot(x)#
Hence:
#1/4int csc^2(u)du = -1/4cot(u) + C#
#u = sin^(-1)(x/2)#
#therefore I = -1/4cot(sin^(-1)(x/2)) + C#
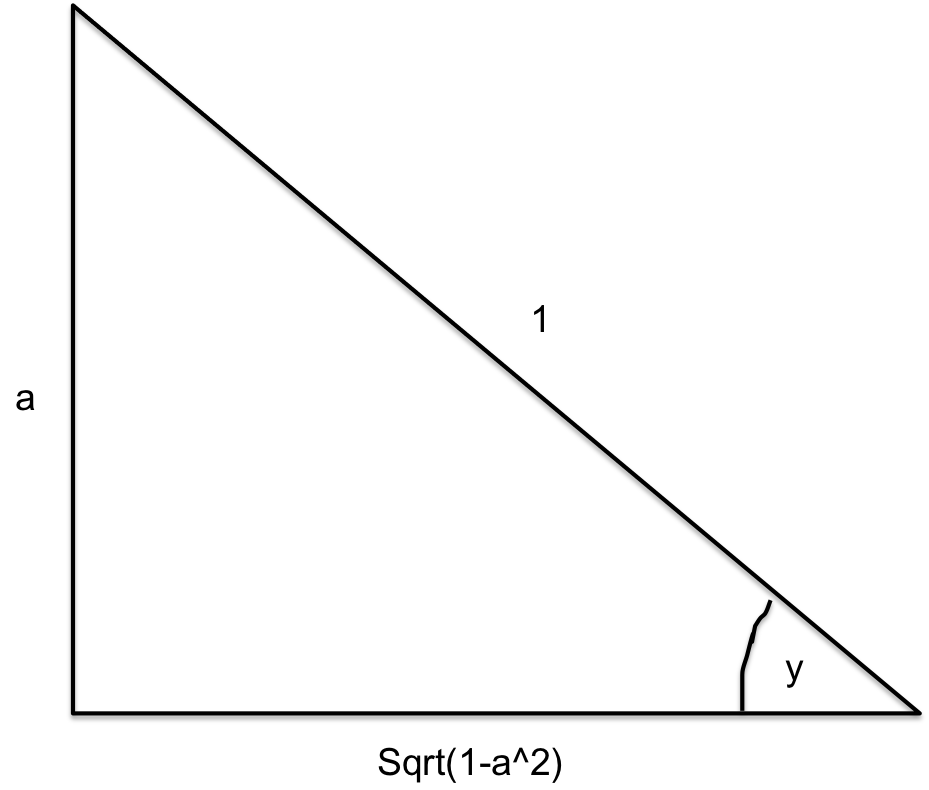
This can look a little scary but it's actually quite simple, we just need to draw a triangle.
Consider #y = sin^(-1)(a)#
#implies a = sin(y)#
Sine is Opposite/Hypotenuse so we have triangle with opposite side #a# and Hypotenuse equal to #1#. Can work out the other side with pythagoras' to be #sqrt(1-a^2)#.
Now, the tangent function is opposite/adjacent, hence:
#tan(y) = (a)/(sqrt(1-a^2))#
#cottheta = 1/(tantheta) implies cot(y) = (sqrt(1-a^2))/(a)#
So #-1/4cot(sin^(-1)(x/2)) = -1/4(sqrt(1-(x/2)^2))/(x/2)#
#=-1/2(sqrt(1-(x^2/4)))/(x) = -1/4(sqrt(4-x^2))/x = -(sqrt(4-x^2))/(4x)#


