Use the rational root theorem and the remainder theorem to determine a zero.
The possible factors in #y = ax^n + bx^(n - 1) + ... + p# are given by #"factors of p"/"factors of a"#.
In our example, these would be #+-1, +-5/3, +-5/1 +-1/3 -> +-1, +-5/3 +-5, +-1/3#.
We now use the remainder theorem to determine the remainder after substituting these values into the function. If the remainder equals 0, we have a factor.
#f(-1) = 3(-1)^4 - 10(-1)^3 - 24(-1)^2 - 6(-1) + 5#
#f(-1) = 3(1) - 10(-1) - 24(1) + 6 + 5#
#f(-1) = 3 + 10 - 24 + 6 + 5#
#f(-1) = 0#
Hence, #-1# is a factor. Next, we need to use synthetic division to divide #3x^4 - 10x^3 - 24x^2 - 6x + 5# by #x + 1#
#-1"_|"3" "-10" "-24" "-6" 5"#
#" "-3" "13" "11" "-5"#
#"-----------------------------------------------------------------------------"#
#" "3" "-13" "-11" "5" 0 "#
Hence, the quotient is #3x^3 - 13x^2 - 11x + 5#.
We repeat the process to find that #-1# is once again a factor. We divide synthetically again, to obtain the result of #3x^2 - 16x + 5#.
We can factor this as:
#3x^2 - 16x + 5 = 3x^2 - 15x - x + 5 = 3x(x - 5) - 1(x - 5) = (3x- 1)(x - 5)#
Setting all of these factors to #0#, we have that this function has a root of #x = -1# of multiplicity #2#, and roots of #1/3# and #5# of multiplicity #1#.
Here is the graph of the function.
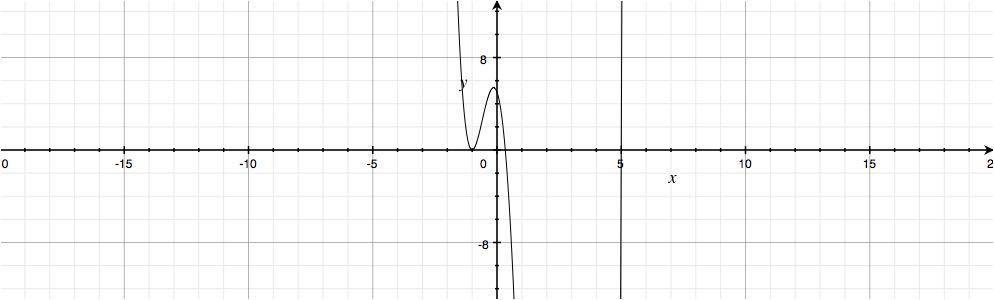
Hopefully this helps!


