Question

How do you find the exact value of `cos45` using the sum and difference, double angle or half angle formulas?

Answer 1

`cos 45^@ = sqrt(2)/2`

Explanation:

The double angle formula for `cos` can be written:

`cos 2theta = cos^2 theta - sin^2 theta = 2cos^2 theta - 1`

Given:

`cos 90^@ = 0`

Let `theta = 45^@` to get:

`0 = cos 90^@ = 2cos^2 45^@-1`

Add `1` to both ends to get:

`1 = 2cos^2 45^@`

Divide both sides by `2` and transpose to find:

`cos^2 45^@ = 1/2`

Hence:

`cos 45^@ = +-sqrt(1/2) = +-sqrt(2/4) = +-sqrt(2)/2`

Now `45^@` is in Q1, so `cos 45^@ > 0` and we need the positive square root.

So:

`cos 45^@ = sqrt(2)/2`

`color(white)()`
Note

I prefer to find `cos 45^@` by considering a `1:1:sqrt(2)` right angled triangle, formed by cutting a square diagonally in half...

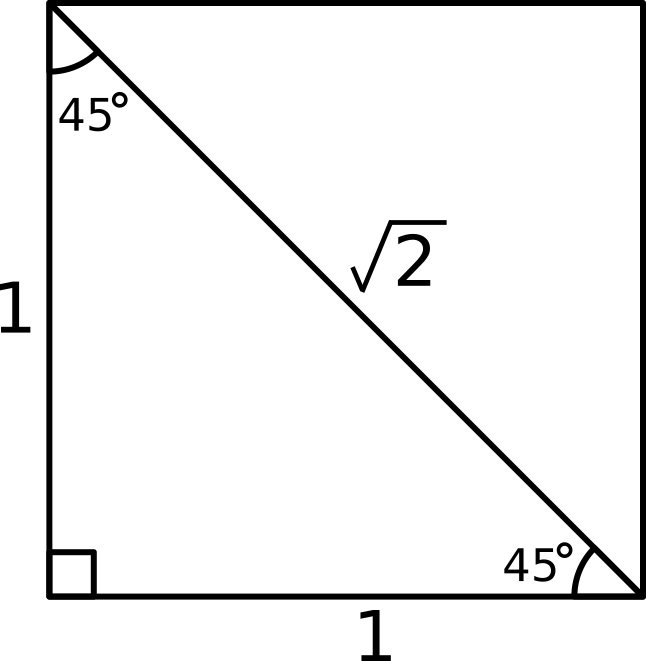
Then:

`cos 45^@ = "adjacent"/"hypotenuse" = 1/sqrt(2) = sqrt(2)/2`