Question

What is the orbital angular momentum quantum number for the orbital 5`p`?

I don't understand anything about it. I don't know where to start.

Answer 1

`l=1`

Explanation:

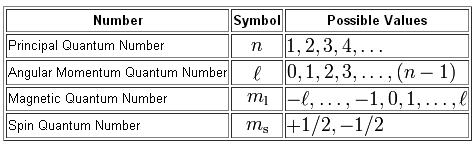
The first thing to note here is that you don't need to know the value of the principal quantum number, `n`, to answer this question.

In other words, you don't need to know the energy level on which the electron resides, which in this case would be `n=5`, to say that the angular momentum quantum number, `l`, for a `p` subshell is equal to `1`.

The `5p` subshell given to you is described by two quantum numbers

• `n=5 ->` this means that the electron is located on the fifth energy level

• `p ->` the means that it is located in the p subshell

Now, the angular momentum quantum number designates the identity of the subshell in which the electron is located

• `l = 0 ->` the s subshell
• `l=1 ->` the p subshell
• `l=2 ->` the d subshell
• `l=3 ->` the f subshell
• `vdots`

In this case, the angular momentum quantum number must be equal to `1` because `1` is the value that describes the `p` subshell for any electron located on an energy level that is `n > 1`.

As you can see from the table, for `n=1`, `l` can only take one value, `l=0`. This means that the first energy level holds `1` subshell, the `s` subshell.

By comparison, for `n=5`, `l` can take

`n = 5 implies l = {0, 1, 2, 3,4 }`

The fifth energy level holds `5` subshells, and `l=1` describes the `p` subshell regardless of the value of `n > 1`.