What is #cos(sin^(-1)(sqrt(2)/2))# ?

Question

8119 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-10-12T23:46:12

#cos(sin^(-1)(sqrt(2)/2)) = sqrt(2)/2#

Note that #cos^2 theta + sin^2 theta = 1#

Hence:

#cos theta = +-sqrt(1-sin^2(theta))#

So if #sin theta = sqrt(2)/2# then:

#cos theta = +-sqrt(1 - (sqrt(2)/2)^2) = +-sqrt(1-1/2) = +-sqrt(1/2) = +-sqrt(2)/2#

Note also that #sin^(-1) x# is always in the range #[-pi/2, pi/2]# and #cos theta >= 0# for #theta in [-pi/2, pi/2]#.

Hence we want the positive square root and we find:

#cos (sin^(-1) (sqrt(2)/2)) = sqrt(2)/2#

Alternatively, just consider a right angled triangle formed by bisecting a unit square diagonally, with sides #1, 1, sqrt(2)#...

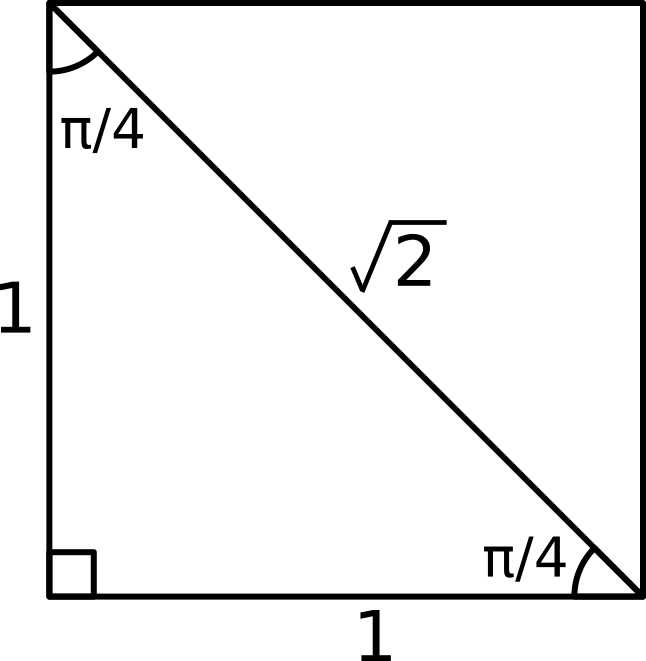
enter image source here

Remember that:

#sin theta = "opposite"/"hypotenuse"#

#cos theta = "adjacent"/"hypotenuse"#

So we can see from this triangle that:

#sin (pi/4) = cos (pi/4) = 1/sqrt(2) = sqrt(2)/2#

Since we are dealing with angles in Q1, we find:

#cos(sin^(-1)(sqrt(2)/2)) = sqrt(2)/2#

Answer 2 · 2016-10-12T23:49:58

#cos(sin^(-1)(sqrt(2)/2))=sqrt(2)/2#

We can solve this using that #sin(pi/4) = sqrt(2)/2# is well known, giving

#sin^(-1)(sqrt(2)/2) = pi/4#

#=> cos(sin^(-1)(sqrt(2)/2)) = cos(pi/4) = sqrt(2)/2#

However, let's look at a more general method for solving this kind of problem.

Suppose we are trying to find #cos(sin^(-1)(x))#. First, draw a right triangle with an angle #a# such that #sin(a) = x#, that is, #a = sin^(-1)(x)#.

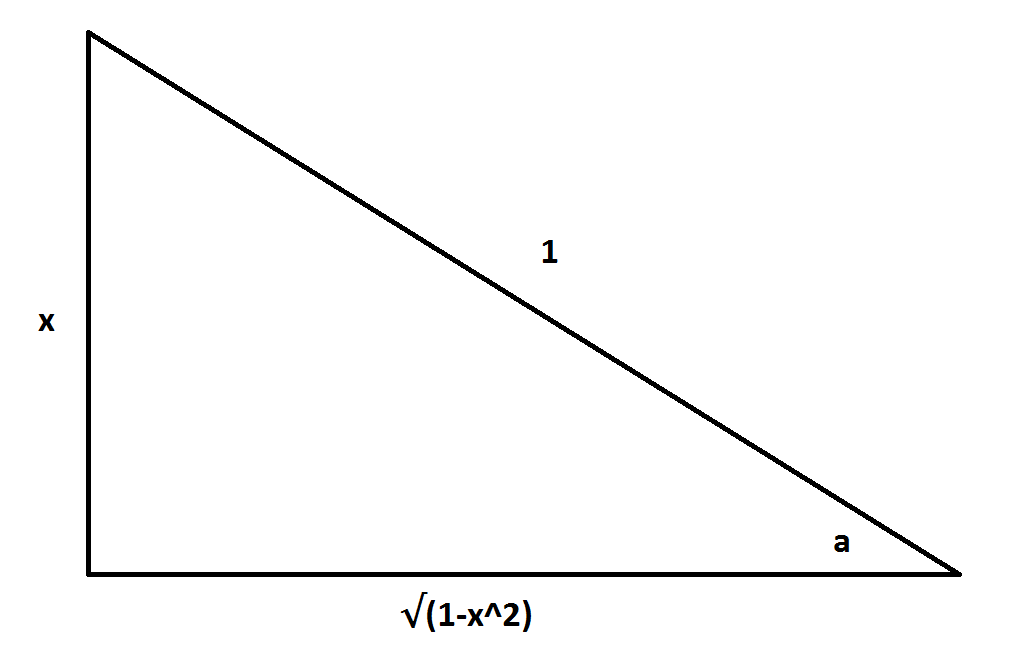
enter image source here

Using the Pythagorean theorem, we can find the remaining side as #sqrt(1-x^2)#. With this, we have

#cos(sin^(-1)(x)) = cos(a) = sqrt(1-x^2)/1 = sqrt(1-x^2)#

If we set #x = sqrt(2)/2#, we find

#cos(sin^(-1)(sqrt(2)/2)) = sqrt(1-(sqrt(2)/2)^2)#

#=sqrt(1-1/2)#

#=sqrt(1/2)#

#=1/sqrt(2)#

#=sqrt(2)/2#

giving us the same answer as above.