Question

Question #0d7b8

Answer 1

i) see below
ii) In the graph of an even function the left side relative to the Y-axis is a reflection of the right side (relative to the Y-axis),
`sin(x)` is not an even function.

Explanation:

i) using the identity: `cos(A-B)=cos(A) * cos(B) - sin(A) * sin(B)`

`cos(-x)=cos(0-x)`

`color(white)("XXX")=cos(0) * cos(x) - sin(0) * sin(x)`

`color(white)("XXX")= 1 * cos(x) - 0 * sin(x)`

`color(white)("XXX")= cos(x)`

ii) Note that the reflection of the right side of `sin(x)` is not equal to `sin(x)`

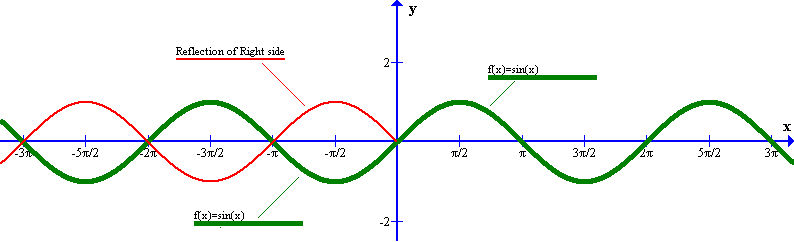
Therefore `sin(x)!=sin(-x)`
and `sin(x)` is not an even function.

Answer 2

When x is expressed in radian, the Maclaurin series for cos x and sin

x are

,`cos x = 1-x^2/(2!)+x^4/(4!) + ... +(-1)^nx^(2n)/((2n)!)+...` and

`sin x = x - x^3/(3!)+x^5/(5!)+...(-1)^nx^(2n+1)/((2n+1)!)+...`

It follows that `cos(-x)=cos x and sin (-x)--sin x`

If `f(-x)=f(x)`, f is even and if `f(-x)=-f(x)`, f is odd.

So, sine is even and cosine is odd.

For even functions y = f(x), like cos x,

if (x, y) is on the graph, then (-x, y) is on

it. So, the graph is symmetrical about the y-axis.

For odd f like sin x,

if (x, y) is on the graph, so is (x, -y). And so, the graph is

symmetrical about x-axis.