How do you use a power series to approximate int_0^1xtan^-1xdx ?
2 Answers
Explanation:
Let
The power series for
And so we get the integrand by multiplying by
And so replacing the integrand with the power series we have:
Integrating each term gives us:
Applying the limits gives us:
We will need to take sufficient terms to get an answer that is stable to 4dp, which I will perform in Excel as follows;
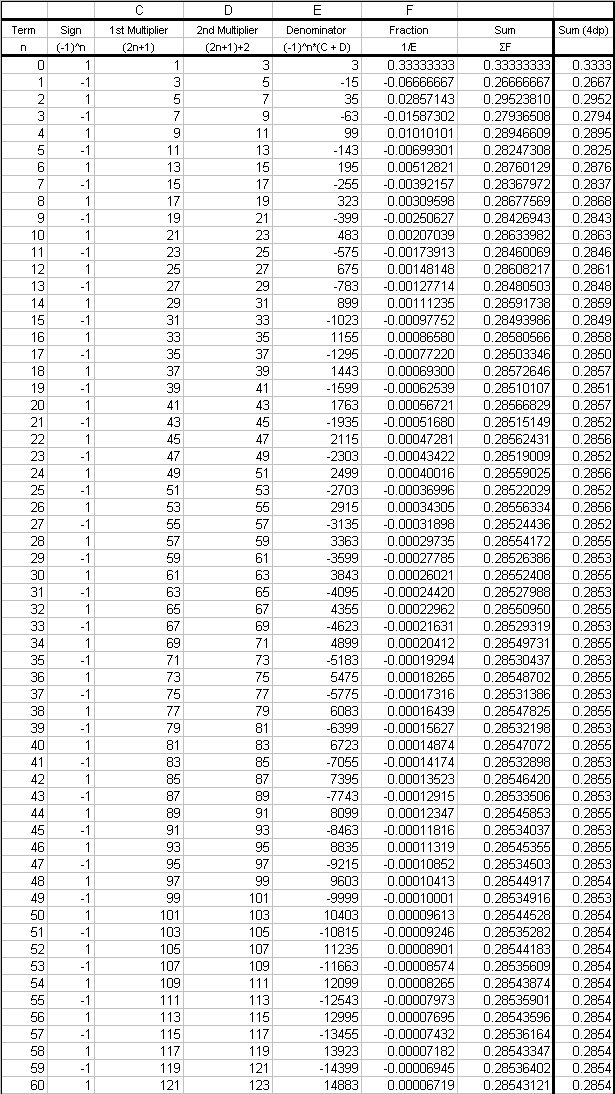
Due to the oscillating natures of the power series it takes a significant number of terms to get a stable answer, but we can conclude that
Explanation:
let
or
then the integral reduces to
now we use the integration by parts
so the integral=
=
now the indefinite integral
so for the limit we get the value of first integral=
similarly the indefinite integral
so for the req. limit we ge
so the ans. is =
=


