Question

What is a quantum harmonic oscillator?

Answer 1

The quantum harmonic oscillator is essentially a two-body problem consisting of two solid spheres connected by a spring.

A basic version of it is called the simple harmonic oscillator (SHO), in which the spring has no dampening factor (no anharmonicity constant):

Since there is no dampening factor, the energy levels are evenly spaced, separated by `ℏomega`, or `hnu` (the anharmonic oscillator would have quadratic convergence of the energy levels). Furthermore, the lowest energy level is `1/2ℏomega`, and not `0`.

The Hamiltonian operator for the SHO system in one dimension is:

`color(blue)(hatH_"SHO") = hatK + hatV`

`= -ℏ^2/(2mu)d^2/(dx^2) + 1/2kx^2`

`= [-iℏd/(dx)]^2/(2mu) + 1/2kx^2`

`= color(blue)(hatp^2/(2mu) + 1/2kx^2)`

where `mu = (m_1m_2)/(m_1 + m_2)` is the reduced mass, `hatp` is the momentum operator, `k` is the force constant, and `x` is the relative displacement from equilibrium. `hatK` and `hatV` were the kinetic and potential energy operators.

The normalized wave function for the `upsilon`th energy level in general is the product of a Hermite polynomial and a decaying exponential.

`color(blue)(psi_(upsilon)(x) = N_(upsilon)H_(upsilon)(sqrtalphax)e^(-alphax^2"/"2))`

where:

• `N_(upsilon) = [1/(2^(upsilon) upsilon!)(alpha/(pi))^"1/2"]^"1/2"` is the normalization constant.
• `H_(upsilon)(sqrtalphax) = (-1)^(upsilon)e^(-alphax^2)d^(upsilon)/(d (sqrtalphax)^(upsilon))[e^(-alphax^2)]` is the Hermite polynomial.
• `alpha = sqrt((kmu)/(ℏ^2))` is a variable defined for convenience of expressing the function.

Applying the variational method on some trial wave function, `psi_0(x) = Ne^(-cx^2)`, where `N = ((2c)/pi)^"1/4"` upon normalization, would give you:

`color(blue)(E_0 = 1/2ℏomega)`

which is in general,

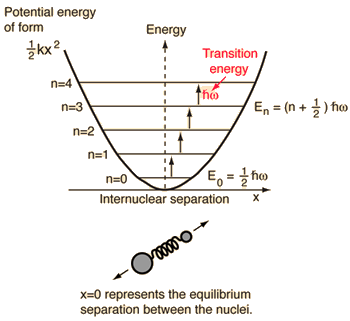
`bb(E_(upsilon) = ℏomega(upsilon + 1/2))`,

as shown in the first image.