How do you find the exact values of the six trigonometric function of #theta# if the terminal side of #theta# in the standard position contains the point (2,1)?

1 Answer
Shell
Nov 6, 2016

Draw a right triangle in the first quadrant using the #x# axis as one of the legs. Find the hypotenuse #r# using the Pythagorean theorem, and then use the values of #x#, #y#, and #r# to find the six trig functions.

Explanation:

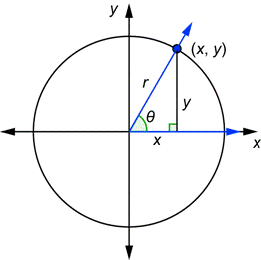
http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final.html

For the point #(2,1)#, #x=2# and #y=1# in the diagram above.

Using the Pythagorean theorem, find #r#.

#x^2 +y^2 = r^2#

#2^2 +1^2 =r^2#

#5=r^2#

#r=sqrt5#

To find the 6 trig functions use #x=2#, #y=1#, #r=sqrt5#

#sintheta=y/r = 1/sqrt5 = sqrt5/5#

#csctheta = 1/sintheta =sqrt5/1 =sqrt5#

#costheta=x/r =2/sqrt5 = (2sqrt5)/5#

#sectheta = 1/costheta = sqrt5/2#

#tantheta=y/x=1/2#

#cottheta=1/tantheta=2/1= 2#

Related questions
See all questions in Trigonometric Functions of Any Angle
Impact of this question
18262 views around the world
You can reuse this answer
Creative Commons License