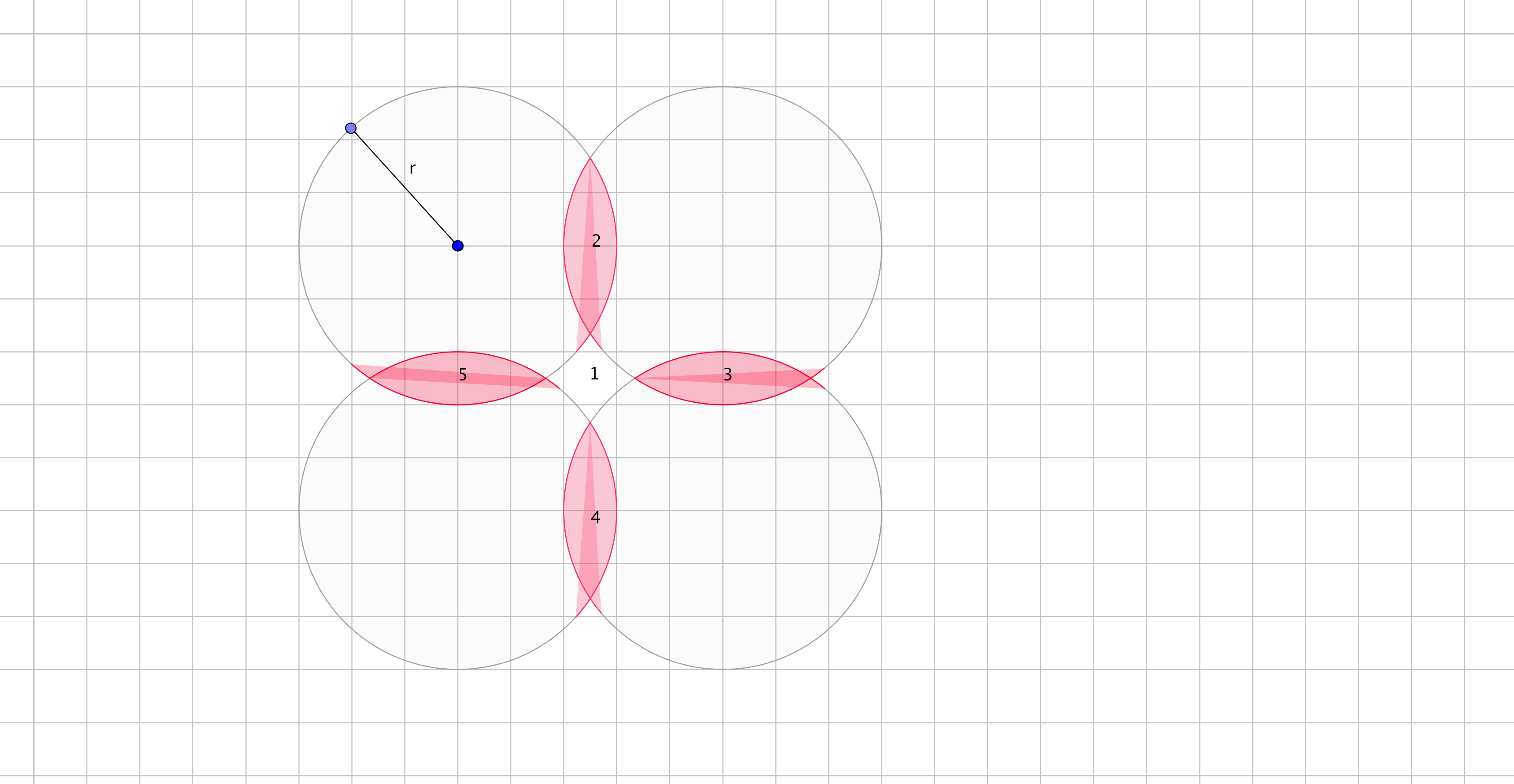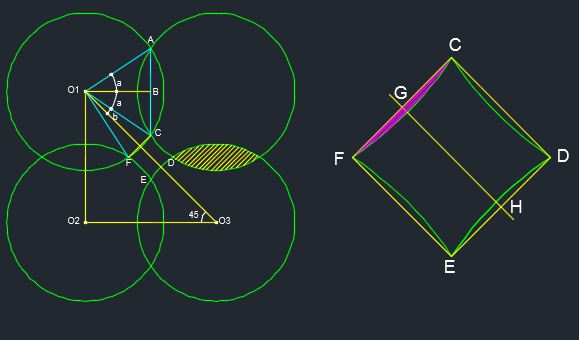
I have to assume that #r=3# units and #O_1O_2=O_2O_3=5# units.
#O_1B=3-0.5=2.5#
#=> cosa=2.5/3, => a=cos^-1(2.5/3)=33.557^@#
Yellow area #(A_Y)# = Area 2 = Area 3 =Area 4 = Area 5
#A_Y=2*(pir^2((2a)/360)-1/2r^2sin2a)#
#=2*9(pi*67.115/360-1/2sin67.115)=2.2508#
#O_1O_2=O_2O_3=5, angleO_2=90^@, => O_1O_3=5sqrt2#
#=> GH=5sqrt2-2r=5sqrt2-2xx3=1.0711#
#b=angleCO_1O_3=45-a=45-33.557=11.443^@#
#O_1G=rcosb=3*cos11.443=2.9404#
#GH=5sqrt2-2*O_1G=5sqrt2-2*2.9404=1.1903#
#GH=CD=DE=EF=FC#
Area of square #CDEF (A_(sq))=1.1903^2=1.4168#
Let the curved square area be #A_(cs)#
Let the red area #(C->F->C)# be #A_R#
#A_R=pir^2*((2b)/360)-1/2r^2sin2b#
#A_R=pi*3^2*(2*11.443)/360-1/2*3^2sin(2*11.443)=0.0475#
#=> A_(cs)=A_(sq)-4*A_R#
#=> A_(cs)=1.4168-4*0.0475=1.227#
Finally, let (Area 1 + Area 2 +Area 3 + Area 4 + Area 5) #= A_T#
#A_T=A_(cs)+4*A_Y=1.227+4*2.2508=10.23# (unit#^2)#