How do you find the number of complex, real and rational roots of #5+x+x^2+x^3+x^4+x^5=0#?
2 Answers
One real root and two pairs of conjugate complex roots.
Explanation:
We have that
includes de roots of
The solution for the real roots of
We know that
Finally the structure for
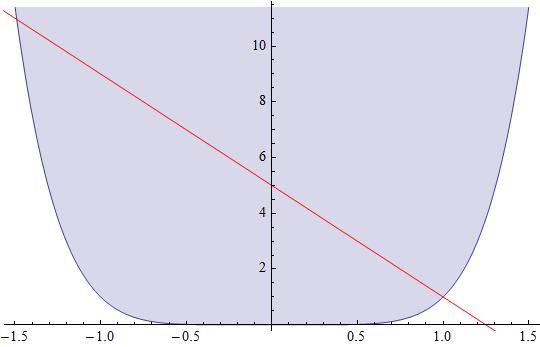
My answer is just to locate the only real root that is negative and close to -1.5 and also the point near (0, 5)
Explanation:
The real root can be bracketed to the desired sd-accuracy by
iterative methods. The 2-sd approximation is
aspects are very clear, in the nice answer by Cesareo R
graph{5+x+x^2+x^3+x^4+x^5 [-23.11, 4.91, -7.01, 6.99]}

