Question

What is the velocity of an electron that makes a transition corresponding to the longest wavelength line of the Lyman series?

Answer 1

`1800kmsec^-1`

Explanation:

Energy of photon `E = (hc)/lamda`

Since `h` and `c` are constants `E` is inversely proportional to wavelength. So in order to get longest wavelength we must choose transition with least energy in Lyman series that is from `2->1`

Finding wavelength

`1/lamda=R(1/1-1/2^2)`

Here value of `R` is approximately `10^7m^-1`

Therefore wavelength `lamda=4/3xx10^-7m`

Energy of photon must be equal to energy of electron

`:.(hc)/lamda=1/2mv^2`

`(6.6xx10^-34xx3xx10^8)/(4/3xx10^-7m)=1/2xx9.1xx10^-31v^2`

After solving velocity `v=1.8xx10^6msec^-1`

or velocity = `1800kmsec^-1`

Answer 2

`1.895 * 10^6"m s"^(-1)`

Explanation:

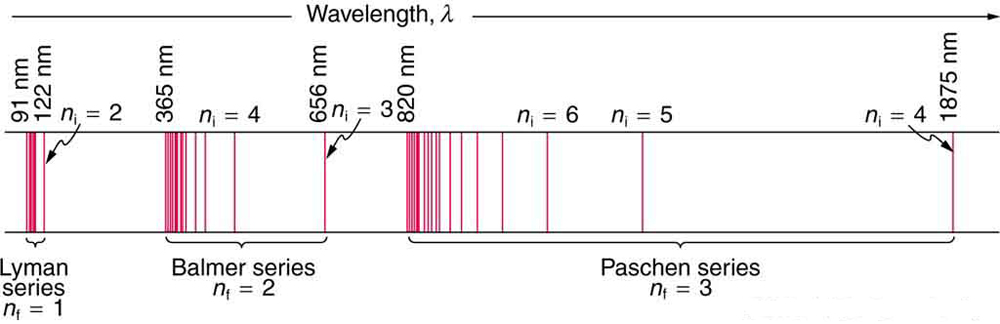
The Lyman series corresponds to the emission lines of a hydrogen atom that has an electron make a transition to the lowest energy level of the electron, which, of course, corresponds to `n=1`.

The trick here is to realize the fact that as an electron moves from an increasingly higher energy level to `n=1`, the energy of the emitted photon Increases.

Simply put, the bigger the difference between `n_i` and `n=1`, the greater the energy of the emitted photon. Now, the energy of a photon is directly proportional to its frequency as given by

`color(blue)(ul(color(black)(E = h * nu))) ->` the Planck - Einstein relation

with

• `E` - the energy of the photon
• `h` - Planck's constant, equal to `6.626 * 10^(-34)"J s"`
• `nu` - the frequency of the photon

Since frequency and wavelength have an inverse relationship as given by

`color(blue)(ul(color(black)(lamda * nu = c)))`

with

• `c` - the speed of light in a vacuum, equal to `"299,792,458 m s"^(-1)`

you can say that the energy of the photon is inversely proportional to its wavelength. In other words, the longer the wavelength, the less energetic the photon.

This implies that the longest wavelength line in the Lyman series will correspond to the lowest energy emission. Therefore, you can say that

`n=2 -> n=1`

The lowest energy emission corresponds to the longest wavelength

Now all you have to do is use the Rydberg equation to find the needed wavelength.

`color(blue)(ul(color(black)(1/(lamda) = R_(oo) * (1/n_f^2 - 1/n_i^2)`

with

• `R_(oo) ~~ 1.097373 * 10^7"m"^(-1)`
• `n_f = 1`
• `n_i = 2`

Rearrange to solve for `lamda`

`lamda = 1/(R_(oo) * (1 - 1/n_i^2))`

Plug in your values to find

`lamda = 1/(1.097373 * 10^(7)"m"^(-1) * (1 - 1/4)) = 1.215 * 10^(-7)"m"`

This corresponds to the actual value of the wavelength, which is equal to approxiamtely `"122 nm"`.

Now, in order to find the velocity of the electron, you must use the fact that its kinetic energy must equal the energy of the emitted photon.

The kinetic energy lost by the electron while making a transition from a higher energy level to a lower energy level is equal to the energy of the emitted photon.

`E_"photon" = E_"kinetic"`

This will get you

`h * nu = 1/2 * m * v^2`

Use the wavelength of the photon to write

`h * c/(lamda) = 1/2 * m * v^2`

The mass of the electron in kilograms is

`m ~~ 9.1094 * 10^(-31) "kg"`

Rearrange the above equation to solve for `v`

`v^2 = (2 * h * c)/(lamda * m) implies v = sqrt((2 * h * c)/(lamda * m))`

Plug in your values to find -- keep in mind that you have

`"1 J" = "1 kg m"^2 "s"^(-2)`

and so the units for Planck's constant are

`"J" * "s" = "kg m"^2"s"^(-2) * "s" = "kg m"^2"s"^(-1)`

`v = sqrt( (2 * 6.626 * 10^(-34) color(red)(cancel(color(black)("kg"))) "m"^2"s"^(-1) * 299,792,458 color(red)(cancel(color(black)("m"))) "s"^(-1))/(1.215 * 10^(-7)color(red)(cancel(color(black)("m"))) * 9.1094 * 10^(-31)color(red)(cancel(color(black)("kg")))))`

`v = "1,894,602.2 m s"^(-1)`

Rounded to four sig figs and expressed in scientific notation, the answer will be

`v = color(darkgreen)(ul(color(black)(1.895 * 10^6"m s"^(-1))))`