Kinetic Energy Question?
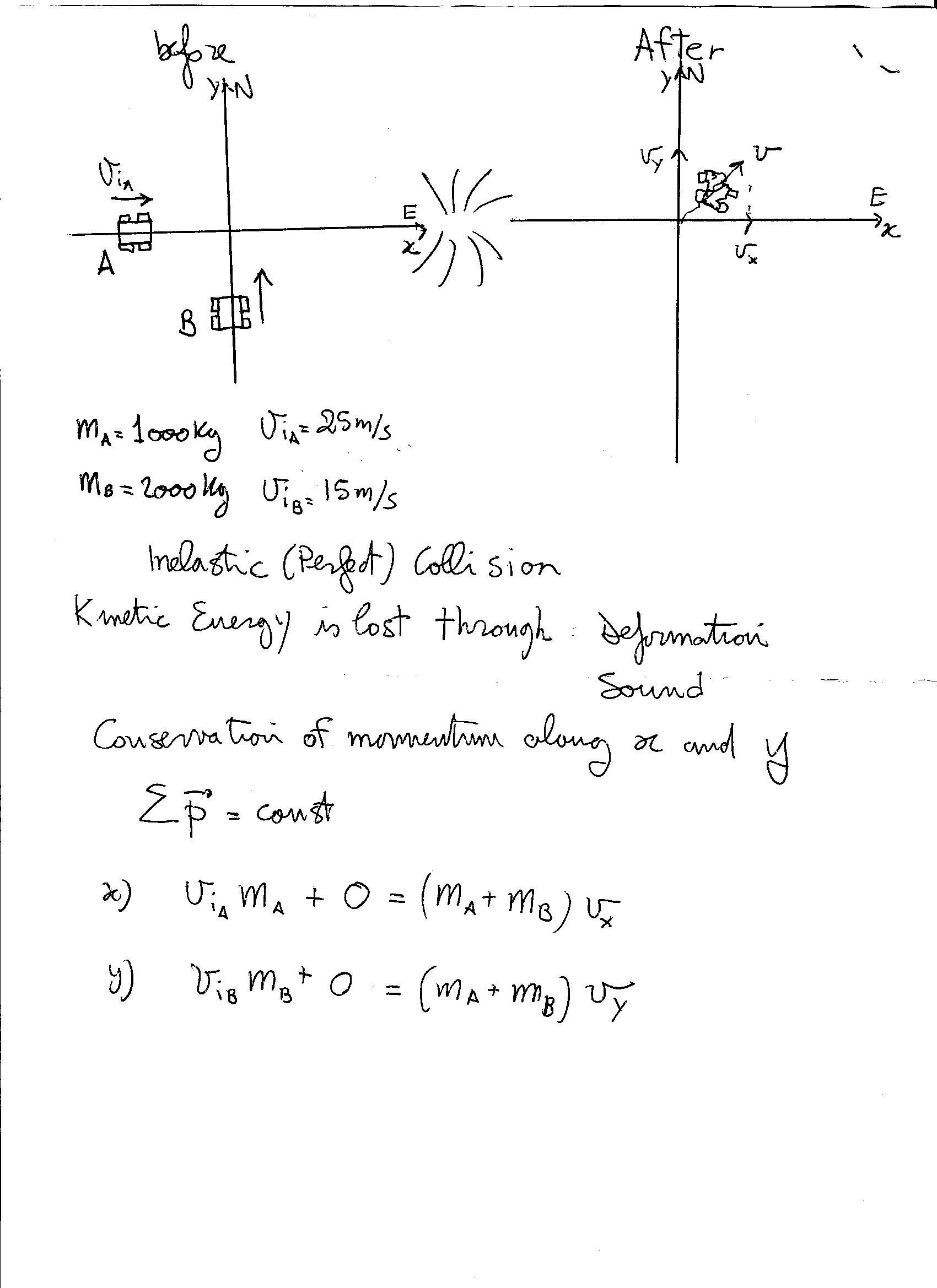
Car A with a mass of 1000kg is travelling east at 25m/s when it collides with car B, 2000kg, travelling north at 15m/s. After the collision, the two cars stick together and have the same velocity. Assume that they slide without friction after collision.
(a) What is the final velocity of the combined mass of cars (magnitude and direction)?
(b) How much kinetic energy was lost in this process and where did it go?
Car A with a mass of 1000kg is travelling east at 25m/s when it collides with car B, 2000kg, travelling north at 15m/s. After the collision, the two cars stick together and have the same velocity. Assume that they slide without friction after collision.
(a) What is the final velocity of the combined mass of cars (magnitude and direction)?
(b) How much kinetic energy was lost in this process and where did it go?
2 Answers
Hi, have a look and try to evaluate it...I cannot finish it now!
Explanation:
have a look and try evaluate
See below.
Explanation:
In the absence of external forces
Here we have
so
so
with
Kinetic energy before
Kinetic energy after
so


