A rectangular poster is to contain 108cm^2 of printed matter with margins of 6cm at the top and bottom and 2 cm on the sides. what's the least cost to make the poster if the printed material costs 5 cents/cm^2 and the margins are 1 cent/cm^2?
1 Answer
The least cost occurs when we have poster dimensions of 10cm x 30cm, leading to a cost of $8.28
Explanation:
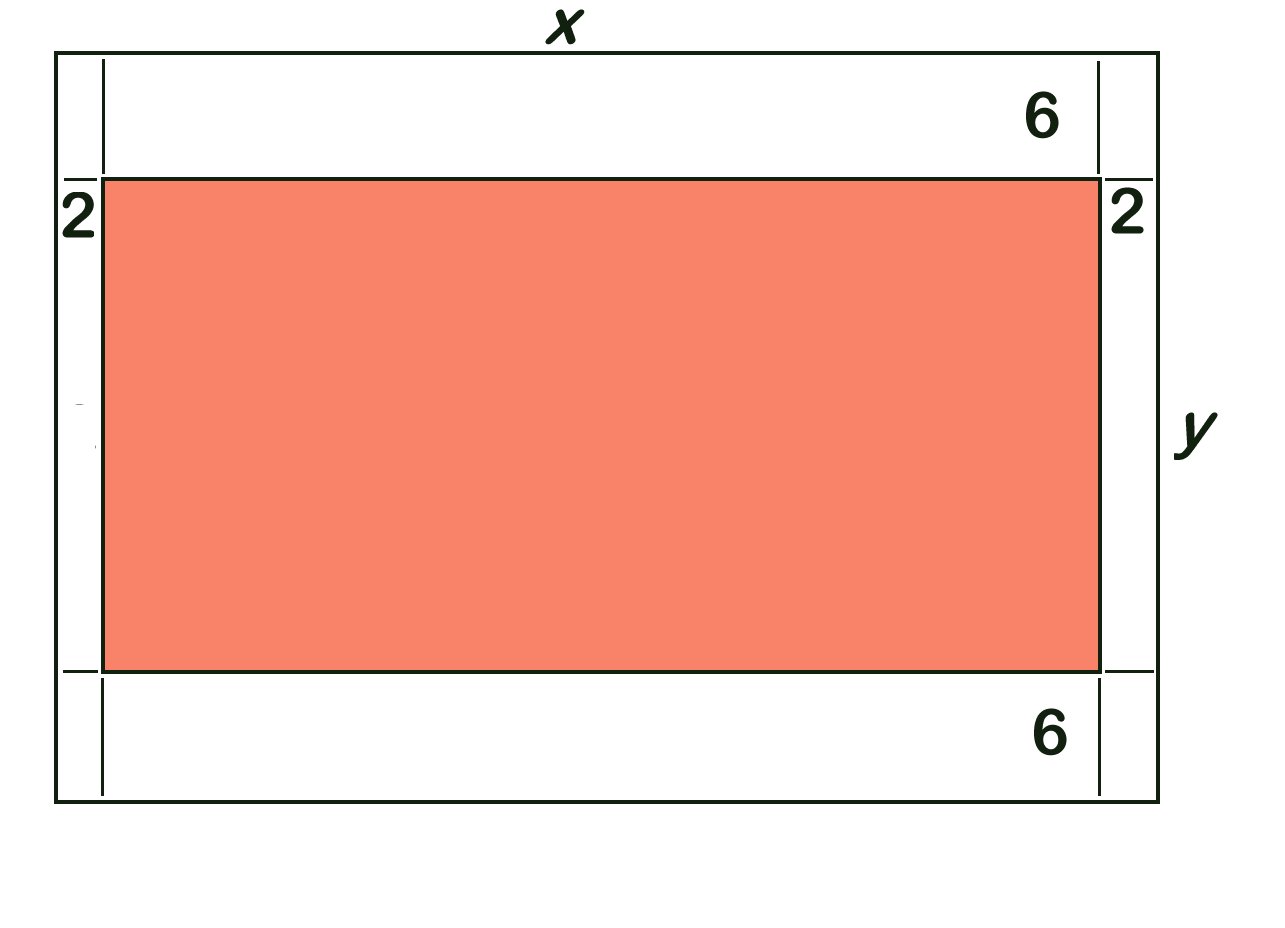
Let us set up the following variables:
# {(x, "Width of poser (cm)"), (y, "Height of poster (cm)"), (P, "Printing cost (cents)") :} #
Then the dimensions of the printed matter are:
# {("Width", =x-2-2,=x-4), ("Height", =y-6-6,=y-12), ( :. " Area",=108 ,=(x-4)(y-12)) :} #
Then the dimensions (Hence Area) of the margins are:
# {(2 xx "Left/Right", =2*2*y,=4y), (2 xx "Top/Bottom", =2 * 6 * x,=12x) , (4 xx "Corners", =4 * 2*6,=48),( :. " Area", ,=4y+12x+48) :} #
Then:
# (x-4)(y-12)=108#
# :. (y-12)=108/(x-4)#
# :. y=12+108/(x-4)#
And so we can form the cost of the poster:
# C = "cost of printed at 5c" + "cost of margins at 1c" #
# :. C = 108*5 + (4y+12x+48)*1#
# :. C = 540 + 4y+12x+48 #
# :. C = 588 + 4y+12x #
# :. C = 588 + 4(12+108/(x-4))+12x #
# :. C = 588 + 48+432/(x-4)+12x #
# :. C = 636+432/(x-4)+12x #
We want to minimize (hopefully) by finding
# (dC)/dx = 0 -432/(x-4)^2+12 #
# (dC)/dx = -432/(x-4)^2+12 #
At a min or max
# :. -432/(x-4)^2+12 = 0 #
# :. 432/(x-4)^2 = 12 #
# :. 36/(x-4)^2 = 1 #
# :. (x-4)^2 = 36 #
# :. (x-4) = +-6 #
# x = 4+-6 #
# :. x = -2,10 #
Obviously
When
# :. 6(y-12)=108 #
# :. y-12=18 #
# :. y=30 #
Hence
With these dimensions we have:
# C = 636+432/(6)+120 = 828# cents
We should check that this value leads to a minimum (rather than a maximum) cost. As the size of the poster is finite this should really be intuitive. We could calculate the second derivative and verify that
graph{636 + 432/(x-4) + 12x [-2, 25, -2560, 2560]}
Hopefully you can visually confirm that a minimum does indeed occur when

