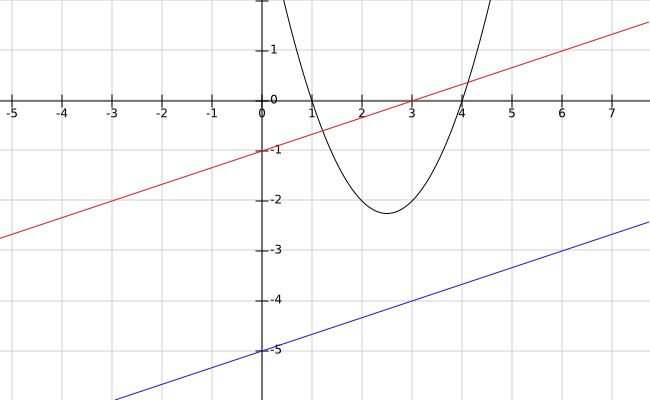
How do you find the equation of the normal line to the parabola #y=x^2-5x+4# that is parallel to the line #x-3y=5#?

Question

13648 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-02T01:48:39

The normal is:

#y=1/3(x-1)#

The general equation of the normal line is:

#y(xi) -f(x) = - 1/(f'(x))(xi-x)#

If we put the equation of the line in the same form:

#y=1/3(x-5)#

we can see the two lines are parallel when

#-1/(f'(x)) = 1/3#

#f'(x) = -3#

Take the derivative of f(x):

#f'(x) = 2x-5#

and fond the value of #x# for which #f'(x) = -3#

#2x-5=-3#

#x=1#

The desired normal line is:

#y - f(1) = -1/(f'(1))(x-1)#

#y=1/3(x-1)#

enter image source here