What is the maximum volume of the box, given the parameters below?
Given a rectangular sheet of cardboard, 16 in. by 10 in., you are asked to cut off identical squares from each of the four corners of the sheet and then bend up the sides of the remaining cardboard to form a rectangular box.
Given a rectangular sheet of cardboard,
1 Answer
The associated max volume is given by:
V=144 cubic inches
Explanation:
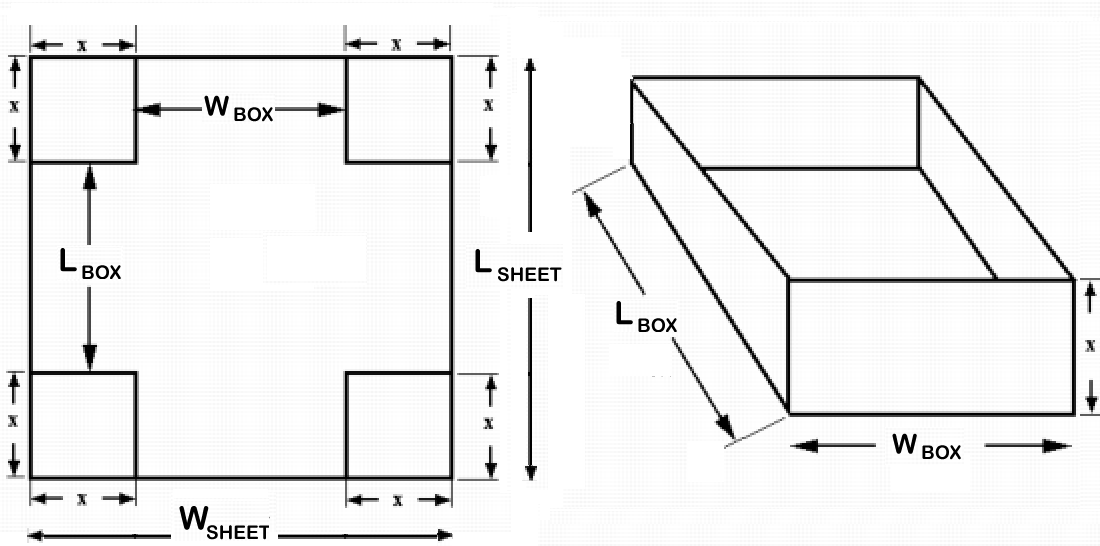
Let us set up the following variables:
{(w, "Width of the Box (in)"), (l, "Length of the Box (in)"), (x, "Length of the Corner Cut-out (in)"), (V, "Volume of the Box (cubic in)") :}
We want to vary the corner length
The dimensions of the sheet are 16" by 10", hence, wlog (without loss of generality) taking
Width:
x+w+x=16 \ \ => w=16-2x = 2(8-x)
Length:x+l+x=10 => l=10-2x = 2(5-x)
Then the volume is given by:
\ \ \ \ \ V=wlx
:. V = 2(8-x)2(5-x)x
:. V = 4x(x^2-13x+40)
:. V = 4x^3-52x^2+160x
Differentiating wrt
:. (dV)/dx=12x^2-104x+160
At a critical point,
:. 12x^2-104x+160 = 0
:. 3x^2-26x+40 = 0
:. (3x-20)(x-2) = 0
:. x=2,20/3 = 0
We should check while value leads to a maximum volume
:. (d^2V)/dx^2=24x-104
x = 2 => (d^2V)/dx^2 < 0 => max
x = 20/3 => (d^2V)/dx^2 > 0 => min
So we have a maximum volume when
V = 4*8-52*4+160*2=32-208+320=144
If we graph the Volume Function,
graph{4x^3-52x^2+160x [-3, 10, -70, 160]}
Hopefully you can visually confirm the above #

