Question

If the ratio of the sides of two similar triangles is 4:9, how do you find the ratio of their areas?

Answer 1

`16:81`

Explanation:

Scale factor for the sides of these triangles. `k =4/9.`

Therefore the ratio of area will be:

`k^2 = "Area Triangle A"/"Area triangle B"`

`k^2 = (4/9)^2`

`= 16/81`

Answer 2

Ratio of their areas is `16:81`.

Explanation:

Let us have two similar triangles `DeltaABC` and `DeltaDEF` as shown below. As they are similar, we have

`(AB)/(DE)=(AC)/(DF)=(BC)/(EF)`

Let us also draw perpendiculars `AP` and `DQ` from `A` and `D` respectively on to `BC` and `EF` as shown.

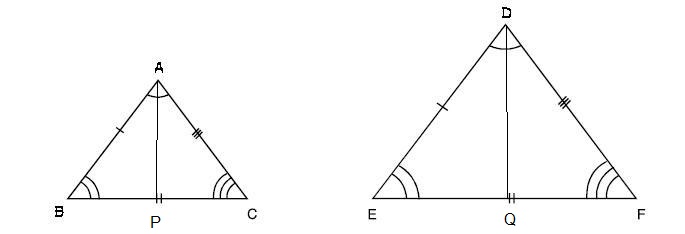
It is apparent that `DeltaAPB` and `DeltaDEQ` are also similar as all respective angles are equal. Hence,

`(AB)/(DE)=(AP)/(DQ)=(BP)/(EQ)`

We also have `DeltaABC=1/2xxBCxxAP` and `DeltaDEF=1/2xxEFxxDQ` and

`(DeltaAPB)/(DeltaDEQ)=(BCxxAP)/(EFxxDQ)=(BC)/(EF)xx(AP)/(DQ)`

But `(AP)/(DQ)=(AB)/(DE)=(BC)/(EF)` and hence

`(DeltaAPB)/(DeltaDEQ)=(BC)/(EF)xx(BC)/(EF)=(BC^2)/(EF^2)` and as

`(BC)/(EF)=(AC)/(DF)=(AB)/(DE)`

`(DeltaAPB)/(DeltaDEQ)=(AC^2)/(DF^2)=(BC^2)/(EF^2)=(AB^2)/(DE^2)`

Hence if sides of two similar triangles are in the ratio `a:b`, their areas are in the proportion `a^2:b^2`

As in given case sides are in the ratio of `4:9`.

ratio of their areas is `4^2:9^2` or `16:81`.