A plane flying horizontally at an altitude of 1 mi and a speed of 540 mi/h passes directly over a radar station. How do you find the rate at which the distance from the plane to the station is increasing when it is 5 mi away from the station?

Question

41661 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-23T20:33:48

Rate# ~~ 529.1 # mi/hour

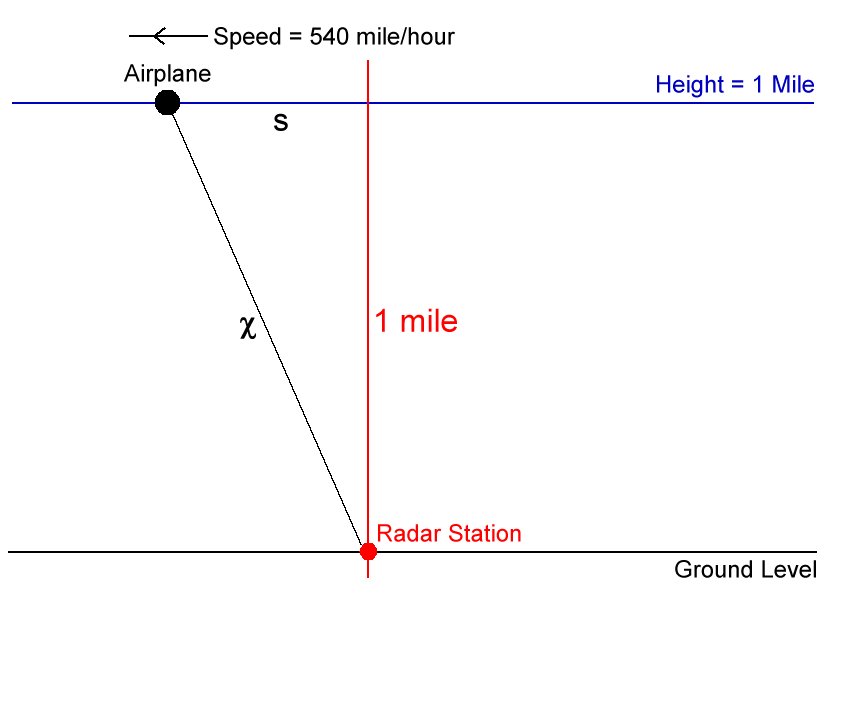
enter image source here

Let us set up the following variables:

# {(s, "Horizontal distance of plane from the radar station (mi)"), (x, "Actual direct distance of plane from the radar station (mi)") :} #

Then, our aim is to find #dx/dt# when #x=5#

The plane is moving in the horizontal direction at constant speed (#540# mi/hour). i.e #(ds)/dt=540#

By Pythagoras;

# \ \ \ \ \ x^2 = s^2+1^2 #
# :.x^2 = s^2+1 # ..... [1]

Differentiating Implicitly wrt #t# we get:

# 2xdx/dt = 2s(ds)/dt + 0 #
# \ \ xdx/dt = s(ds)/dt #
# \ \ xdx/dt = 540s #
# \ \ xdx/dt = 540sqrt(x^2-1) " "# (Using [1])

When # x=5 => #

# \ \ \ \ \ 5dx/dt = 540sqrt(25-1) #
# :. 5dx/dt = 540sqrt(24) #
# :. dx/dt = 108sqrt(24) #
# :. dx/dt ~~ 529.1 # mi/hour