Question

What is the normal to the tangent line at the y-intercept to `y = 1/3x^3 - 4x + 2`?

Answer 1

`y = 1/4x + 2`

Explanation:

The y-intercept will occur at `(0, 2)`:

`y = 1/3(0)^3 - 4(0) + 2 = 2`

The function's derivative can be found by the power rule, which states that `d/dx(x^n) = nx^(n - 1)`.

`y' = x^2 - 4`

The slope of the tangent is given by evaluating your point `x= a` into the derivative. The normal line is perpendicular to the tangent line, or the product of their two slopes equals `-1`.

The slope of the tangent is `m = 0^2 - 4 = 0 - 4 = -4`. Then the slope of the normal line is `1/4`.

Since the reaction passes through `(0, 2)`, the normal line has equation:

`y - y_1 = m(x - x_1)`

`y - 2 = 1/4(x - 0)`

`y - 2 = 1/4x`

`y = 1/4x + 2`

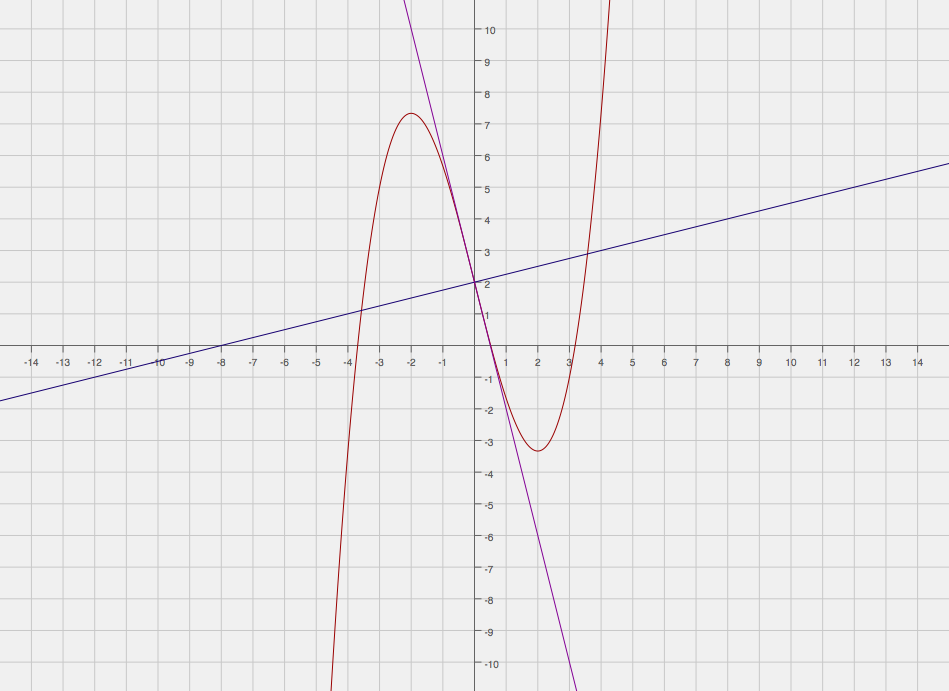
Here is a graphical depiction of the problem. The graph in `color(red)("red")` is the function `y = 1/3x^3 - 4x + 2`, the graph in `color(purple)("purple")` is the tangent line and the graph in `color(blue)("blue")` is the normal line.

Hopefully this helps!