How do you find the volume of the solid bounded by the coordinate planes and the plane 3x + 2y + z = 6?
2 Answers
The answer is
Explanation:
We have here a tetrahedron.
Let's find the vertices,
Let
we get
vertex
Let
We get
vertex
Let
We get
vertex
And the volume is
Where,
Volume = 6 (
Explanation:
The coordinate planes are given by
The given tetrahedron is a solid that lies above the triangle
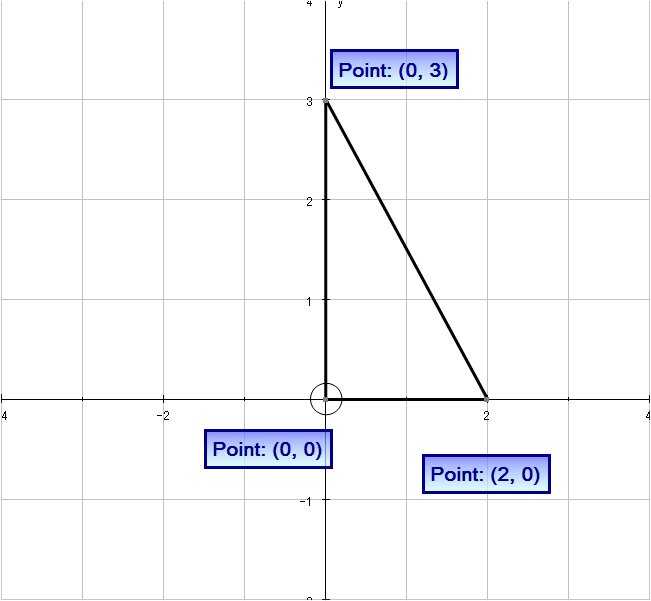
The line joining
# y-0 = (3/-2)(x-2) #
# :. y = -3/2x+3 #
And so the region
# R = {(x, y) | 0 le x le 2, 0 le y le −3/2x +3 } #
And the volume,
integral of the function
# :. V = int int_R (6 − 3x − 2y) \ dA#
# " "= int_0^2 int_0^(-3/2x+3) (6 − 3x − 2y) \ dy \ dx#
# " "= int_0^2 [(6-3x)y-y^2]_(y=0)^(y=-3/2x+3) \ dx #
# " "= int_0^2 {(6-3x)((-3x)/2+3)-((-3x)/2+3)^2} - {0} \ dx #
# " "= int_0^2 (-9x+18+9/2x^2-9x)-(9/4x^2-9x+9) \ dx #
# " "= int_0^2 (-9x+9+9/4x^2) \ dx #
# " "= [-9/2x^2+9x+9/12x^3]_0^2 #
# " "= {-18+18+72/12} - {0} #
# " "= 6 #


