Question

How would you find the volume of the tetrahedron T bounded by the coordinate planes and the plane 3x+4y+z=10?

Answer 1

Volume = 125/9 (`"units"^3`)

Explanation:

The coordinate planes are given by `x = 0`, `y = 0` and `z = 0`. The volume is that of a tetrahedron whose vertices are the intersections of three of the four planes given. The intersection of `x = 0`, `y = 0` and `3x + 4y + z = 10` is `(0, 0, 10)`, Similarly, the other three vertices are `(10/3, 0, 0)`, `(0, 5/2, 0)` and the origin `(0, 0, 0)`.

The given tetrahedron, `T`, is a solid that lies above the triangle `R` in the `xy`-plane that has vertices `(0, 0)`, `(10/3, 0)` and `(0, 5/2)`.

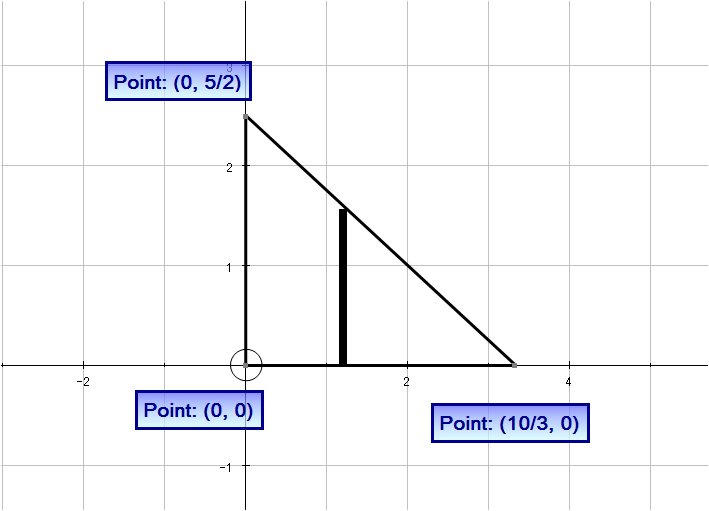
The line joining `(0, 5/2)` and `(10/3, 0)` is given by:

`y-0 = ((5/2)/(-10/3))(x-10/3)`
`:. y = -3/4x+5/2`

And so the region `R` is defined as:

`R = {(x, y) | 0 le x le 10/3, 0 le y le −3/4x +5/2 }`

And the volume, `V`, of the tetrahedron is the double
integral of the function `z=10 − 3x − 4y` over `R`.

`:. V = int int_R (10 − 3x − 4y) \ dA`
`" "= int_0^(10/3) int_(0)^(-3/4x+5/2) (10 − 3x − 4y) \ dy \ dx`
`" "= int_0^(10/3) [(10-3x)y-2y^2]_(y=0)^(y=-3/4x+5/2) \ dx`
`" "= int_0^(10/3) {(10-3x)((-3x)/4+5/2)-2((-3x)/4+5/2)^2} - {0} \ dx`
`" "= int_0^(10/3) (-30/4x+25+9/4x^2-15/2x)-2(9/16x^2-15/4x+25/4) \ dx`
`" "= int_0^(10/3) (-15/2x+25/2+9/8x^2) \ dx`
`" "= [-15/4x^2+25/2x+9/24x^3]_0^(10/3)`
`" "= {-15/4*100/9+25/2*10/3+3/8*1000/27} - {0}`
`" "= -125/3+125/3+125/9`
`" "= 125/9`