How do you find the volume of the solid in the first octant, which is bounded by the coordinate planes, the cylinder #x^2+y^2=9#, and the plane x+z=9?
1 Answer
The volume is
Explanation:
The graphs of the plane
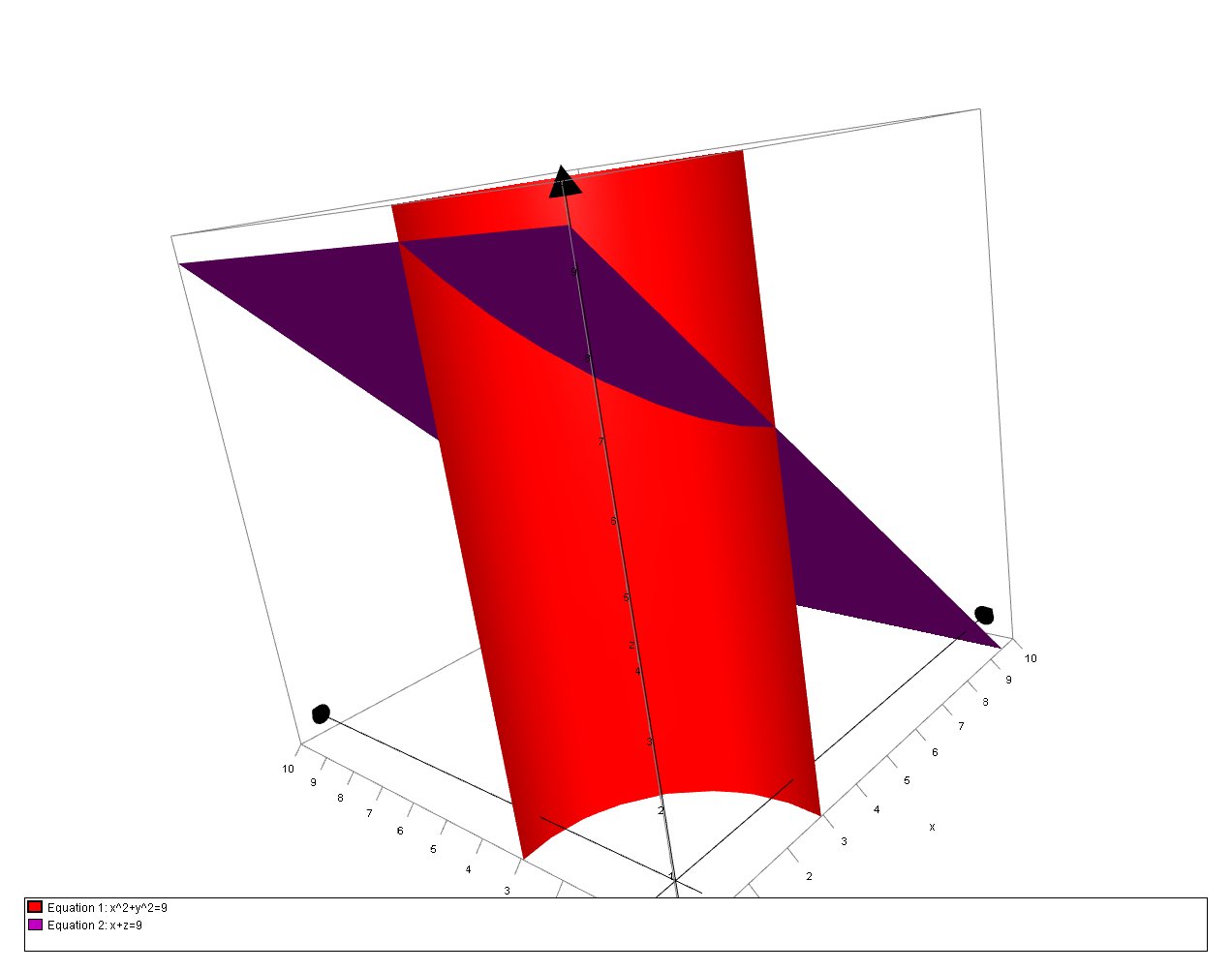
We can us a triple integral to represent the volume as follows:
# v= int int int_R dV#
where
#R={ (x,y,z) | x,y,z>0; x^2+y^2<=9; z<9-x }#
And so we can set up a double integral as follows:
# v= int_a^b int_c^d f(z) \ dx \ dy #
# \ \ = int_a^b int_c^d (9-x) \ dx \ dy #
We now determine the limits of integration by examining a cross section in the
# 0 le x le sqrt(9-y^2)# and# 0 le y le 3#
So our integral for the volume is:
# v= int_0^3 int_0^(sqrt(9-y^2)) (9-x) \ dx \ dy #
With nested integral we evaluate from he inside out, so let's deal with the inner integral;
# int_0^(sqrt(9-y^2)) (9-x) \ dx = [9x-1/2x^2]_0^(sqrt(9-y^2)) #
# " " = 9(sqrt(9-y^2))-1/2(sqrt(9-y^2))^2 #
# " " = 9sqrt(9-y^2)-1/2(9-y^2) #
And so our double integral now becomes:
# v= int_0^3 {9sqrt(9-y^2)-1/2(9-y^2) }\ dy #
And for this integral we can split into the two parts
# I_1 = int_0^3 9sqrt(9-y^2) \ dy# and# I_2 = int_0^3 -1/2(9-y^2) \ dy #
We can just evaluate the second integral to get:
# I_2 = -1/2[ 9y-1/3y^3 ]_0^3 #
# \ \ \ = (-1/2){(9)(3)-1/3(27) - 0} #
# \ \ \ = -9 #
And for the first integral we use the substitution
# I_1 = 9 int_0^3 sqrt(9-y^2) \ dy #
# \ \ \ = 9 [ysqrt(9-y^2)/2 + 9/2 arcsin(y/3) ]_0^3 #
# \ \ \ = 9 {(0+9/2pi/2) - (0+0) } #
# \ \ \ = (81pi)/4 #
NOTE - You may also observe that the above integral
Combining our results gives the total volume as:
# v= (81pi)/4 - 9#
# \ \ = (81pi)/4 - 9#
# \ \ = 54.617251 ... #

