How do you graph #f(x)=x^4-4x^3+x^2+6x#?
1 Answer
I would recommend starting by factoring. We can instantly factor out an
#f(x) = x(x^3 - 4x^2 + x + 6)# .
Now, use the rational root theorem to determine the factors. For a polynomial
#"possible factors" = "(+-1, +-2, +-3, +-6)/(+- 1)#
#"possible factors" = +-1, +-2, +-3, +-6#
I usually start at
The remainder theorem will confirm which of those numbers are factors. If
#f(1) = 1(1^3 - 4(1)^2 + 1 + 6) = 4" "color(red)(xx)#
#f(-1) = 1((-1)^3 - 4(-1)^2 - 1 + 6) =0" "color(green)(√)#
We have a factor. Now use either synthetic or long division to divide
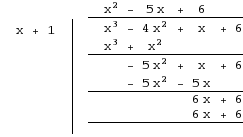
So, we can now write
Hence,
There will be four x-intercepts, at
They all have multiplicity
We will have to repeat the above process to find the zeroes of the derivative, which will be the critical points.
Once you have done this, you should obtain
There will be critical points at
#0 = 2x^2 - 4x - 3#
#x = (-(-4) +- sqrt((-4)^2 - (4 * 2 * -3)))/(2 * 2)#
#x= (4 +- sqrt(40))/4#
#x = (4 +- 2sqrt(10))/4#
#x = 1 +- 1/2sqrt(10)#
Test to the left and right of all of these points, by taking test points and plugging them into the derivative. For example, If they are negative, then the function is decreasing in that interval. If the function is decreasing to the left of the critical point, and increasing to the right, you most certainly have a local minimum, for example.
Doing this, you will find that there are local minimums at
The final step is checking end behaviour. This will be determined by the leading term in the initial polynomial, or
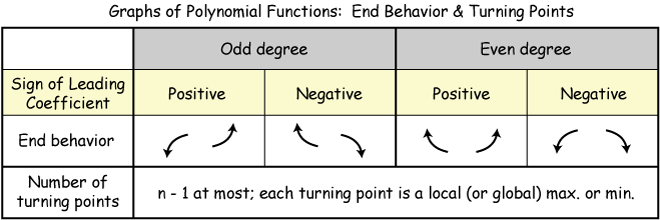
This proves that
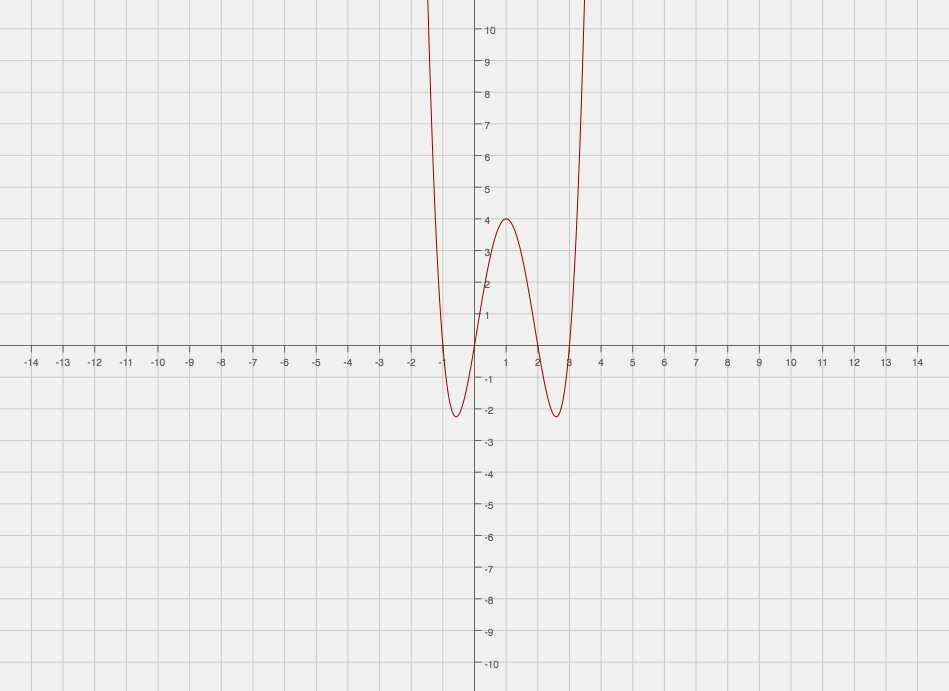
Hopefully this helps!

