A conical paper cup is 10 cm tall with a radius of 30 cm. The cup is being filled with water so that the water level rises at a rate of 2 cm/sec. At what rate is water being poured into the cup when the water level is 9 cm?
1 Answer
Rate
Explanation:
Let us set up the following variables:
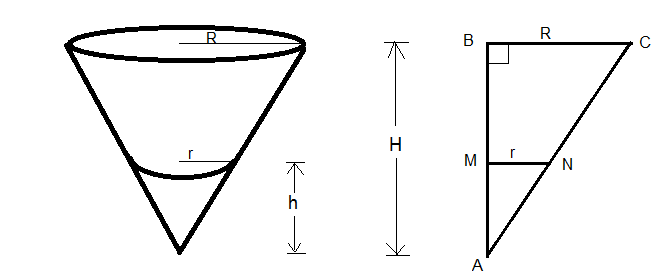
# {(R, "Radius of conical cup (cm)",=30 \ cm), (H, "Height of the conical cup (cm)",=10 \ cm), (t, "time", "(s)"), (h, "Height of water in cup at time t","(cm)"), (r, "Radius of water at time t","(cm)" ), (V, "Volume of water at time t", "(cm"^3")") :} #
Our aim is to find
By similar triangles we have
# r:h = R:H #
# :. r/h=30/10 => r = 3h #
The volume of a cone is
# V = 1/3 pi r^2 h #
# \ \ \ = 1/3 pi (3h)^2 h #
# \ \ \ = 1/3 pi 9h^2 h #
# \ \ \ = 3pi h^3 #
Differentiating wrt
# (dV)/(dh) = 9pih^2 #
And Applying the chain rule we have:
# (dV)/(dt) = (dV)/(dh) * (dh)/(dt) #
# \ \ \ \ \ \ \= 9pih^2 * 2 #
# \ \ \ \ \ \ \= 18pih^2 #
And so when h=9 we have:
# [ (dV)/(dt) ]_(h=9) = 18pi(9^2) = 1458pi \ cm^3s^-1 #

