Question

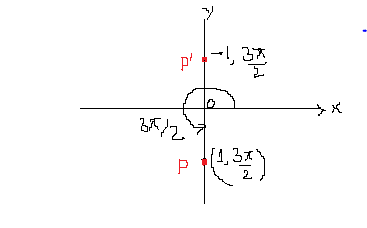
What is the Cartesian form of `(-1,(22pi)/4))`?

Answer 1

(0,1)

Explanation:

First of all, angle `(22pi)/4` is `(11pi)/2` which is equivalent to #4pi +(3pi)/2# that is `(3pi)/2` because `4pi` just adds 0 to the angle `(3pi)/2`

So, first we move by an angle of `(3pi)/2` radians anti-clockwise
around the pole from starting position of 0 radians. This is shown in the figure below, as point P. Now since r= -1, we move in the opposite direction of r=1 for angle of `(3pi)/2` . This positions has been indicated by point P' in the figure.

As is now evident from the figure, cartesean coordinates for`(-1, (22pi)/4)` would be point P' (0,1)