Question

Is there a formula for such a multiple conditional probability?

Answer 1

Yes. The Bayesian statistics allow multiple levels of conditional probability.

Explanation:

If events A and B are not independent, then the probability of the intersection of A and B (the probability that both events occur) is defined by P(A and B) = P(A)P(B|A). Then

P(B|A)=P(A and B)/P(A)

Each term that is conditional on another term must have that probability factor included. Be very careful to identify which event depends upon the other. That is, if P(B) is conditional on P(D), the factor P(B|D) must be calculated to obtain P(B).

To calculate the probability of the intersection of more than two events, the conditional probabilities of all of the preceding events must be considered. In the case of three events, A, B, and C, the probability of the intersection
P(A and B and C) = P(A)P(B|A)P(C|A and B).

For independent events A and B, this is equal to:
`P(B)P(A) + P(B)P(A^c) = P(B)(P(A) + P(A^c)) = P(B)(1) = P(B)`
Since the probability of an event and its complement must always sum to 1. Bayes's formula is defined as follows:

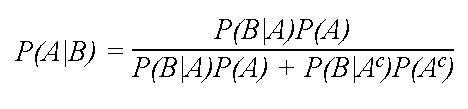
See also: http://www.stat.yale.edu/Courses/1997-98/101/condprob.htm
from which most of this explanation was taken.