Solve the equation # sinx \ cosx = sqrt(2)/4 # for #0 le x le 2pi #?

Question

3288 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-11T23:59:05

# x = pi/8, (3pi)/8, (9pi)/8, (11pi)/8 #

We want to solve:

# sinx \ cosx = sqrt(2)/4 #

We can simplify the expression using the identity;

# sin 2A -= 2sinA \ cos A #

Which gives us:

# \ \ 1/2sin2x = sqrt(2)/4 #
# :. sin2x = sqrt(2)/2 #

If #0 le x le 2pi => 0 le 2x le 4pi#, so we look for solutions of #sin theta = sqrt(2)/2# for #theta in [0,4pi]#

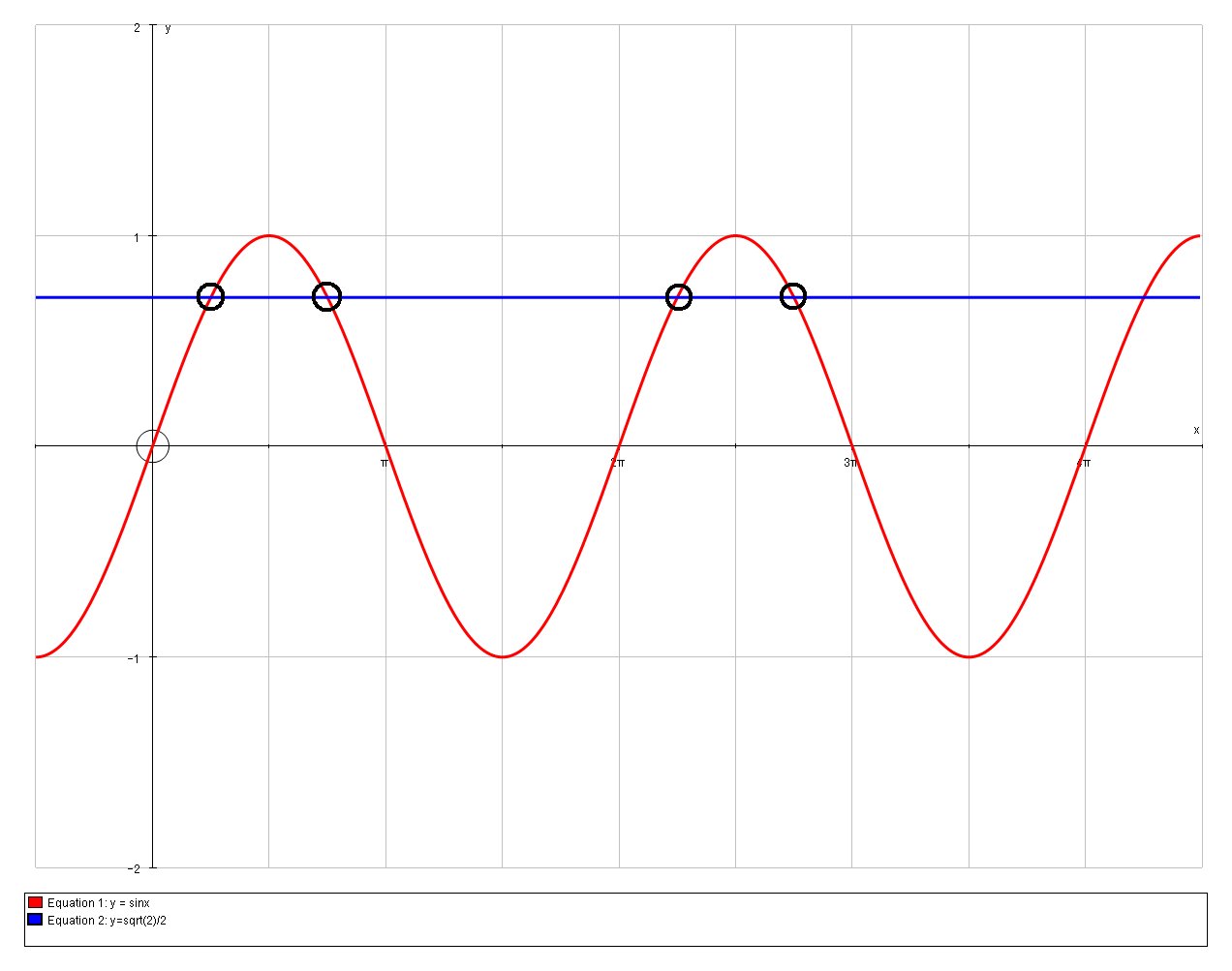
enter image source here

So the solutions within the range #2x in [0,4pi] \ \ (=> x in [0,2pi])# are:

# \ \ \ \ \ 2x = pi/4, pi-pi/4, 2pi+pi/4, 3pi-pi/4 #
# :. 2x = pi/4, (3pi)/4, (9pi)/4, (11pi)/4 #
# :. \ \ x = pi/8, (3pi)/8, (9pi)/8, (11pi)/8 #