Question

How do we arrive at the formula for area of a circle as `pir^2`?

Answer 1

Please see below.

Explanation:

`pi` is defined as the ratio of circumference `C` of a circle to its diameter, which is double the radius `r`, hence by definition

`pi=C/(2r` and `C=2pir`

There are various ways of deriving formula for area of circle, including complicated one using calculus, however the simplest one found extensively on internet involves splitting a circle into smaller and smaller sectors and then rearranging them as shown below

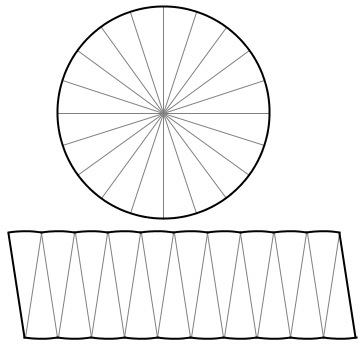
It is apparent that rearrangement forms roughly a rectangle, which becomes more and more accurate, as we divide a circle in to fine sectors, whose width is `r` and length is half the circumference i.e. `pir`

Hence, area of circle is `pirxxr=pir^2`