Question

How do you write the equation of the line through (4,-8) and (8,5)?

Answer 1

`13x-4y=84`

Explanation:

Step 1: Determine the slope of the line through the given points

`"slope"=("change in "y)/("change in "x)`

Given the points, `(x_1,y_1)=(4,-8)` and `(x_2,y_2)=(8,5)`,
the slope, `m` is given by:
`color(white)("XXX")m=(5-(-8))/(8-4)=13/4`

Step 2: Write the equation in slope-point form
Given a slope `m` and a point `(x_1,y_1)`,
the slope-point form of the equation is:
`color(white)("XXX")y-y_1=m(x-x_1)`
In this case we have:
`color(white)("XXX")m=13/4" and "(x_1,y_1)=(4,-8)`
giving
`color(white)("XXX")y-(-8)=13/4(x-4)`

Step 3: Convert into standard form
Standard form of a linear equation is
`color(white)("XXX")Ax+By=C`
Starting from the slope-point form (above) we have:
`color(white)("XXX")4(y+8)=13(x-4)`

`color(white)("XXX")4y+32=13x-52`

`color(white)("XXX")13x-4y=84`

For verification purposes, here is a graph with the given points and the equation `13x-4y=84`

Answer 2

`y=13/4x-21`

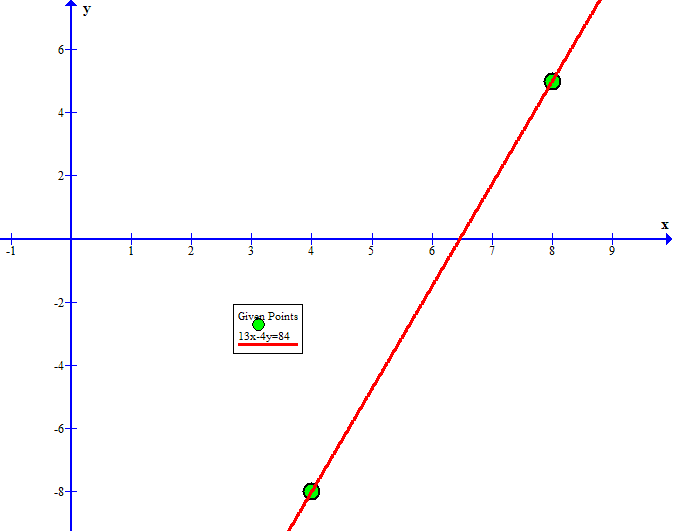
Explanation:

`color(blue)("Preamble")`

consider the standardised equation format of: `y=mx+c`
where `m` is the gradient.

`m=("changing in up or down")/("change in along")`

Very important`->`the change in along (usually the x-axis) is read left to right.

Watch out for this because sometimes questions give the points in the revers order.

So the first point is at say `x_1` and the second point is at say `x_2`. Then `x_1 < x_2`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Answering the question")`

`color(brown)("Determine the gradient")`

Let point 1 be `P_1->(x_1,y_1)=(4,-8)`
Let point 2 be `P_2->(x_2,y_2)=(8,5)`

`m=(y_2-y_1)/(x_2-x_1) = (5-(-8))/(8-4) =(5+8)/(8-4)=13/4`

So we now have:`" "y=13/4x+c`

`color(brown)("Determine the value of the constant "c)`

I chose `P_1 ->`using the value for this point substitute for `x and y`

`y=13/4x+c" "->" "-8=13/4(4)+c`

`c=-8-13=-21`

So we now have:`" "y=13/4x-21`