Question

How many electrons can go into the third quantum level?

Answer 1

`"18 e"^(-)`

Explanation:

A quick way to tackle this question is by using the equation

`color(blue)(ul(color(black)("no. of e"^(-) = 2n^2)))`

Here

• `n` is the principal quantum number

In your case, you will have

`color(darkgreen)(ul(color(black)("no. of e"^(-) = 2 * 3^2 = "18 e"^(-))))`

Now, let's double-check this result by counting the orbitals that are present in the third energy shell.

You know that we can use a total of four quantum numbers to describe the location and spin of an electron in an atom.

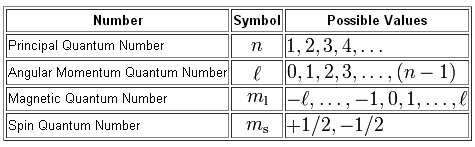
To find the number of electrons that can be located in the third energy shell, which is the energy level that corresponds to `n=3`, we must find the number of orbitals that can exist in this particular energy shell.

For starters, we know that

`n = 3 implies l = {0, 1, 2}`

This means that the third energy shell holds `3` energy subshells, each corresponding to one value of the angular momentum quantum number, `l`.

Now look at the values that correspond to the magnetic quantum number, `m_l`, because these values give you the actual orbitals present in each subshell

• `ul(l = 0 implies m_l = 0) ->` the `l=0` subshell can only hold `1` orbital

• `ul(l=1 implies m_l = {-1, 0 ,1}) ->` the `l=1` subshell can hold `3` orbitals

• `ul(l=2 implies m_l = {-2, -1, 0 ,1, 2}) ->` the `l=2` subshell can hold `5` orbitals

Therefore, you can say that the third energy shell holds a total of

`1 + 3 + 5 = "9 orbitals"`

According to the Pauli Exclusion Principle, each orbital can hold a maximum of `2` electrons*, which means that the maximum number of electrons that can be placed in the third energy shell is

`color(darkgreen)(ul(color(black)("no. of e"^(-) = 2 * 9 = "18 e"^(-))))`