Question

By considering the roots of `z^5 =1`, how do you show that cos(2π/5) + cos(4π/5) + cos(6π/5) + cos(8π/5) = -1?

Answer 1

Please see below.

Explanation:

As `z^5=1=(cos0+isin0)`

According to De-Moivre's theorem

`z=(z^5)^(1/5)=(cos((2npi)/5)+isin((2npi)/5))` and we get five roots of `1` by changing value of `n` from `0` to `4` and we get five roots as

`cos0+isin0`or `1+i0`, `cos((2pi)/5)+sin((2pi)/5)`, `cos((4pi)/5)+sin((4pi)/5)`, `cos((6pi)/5)+sin((6pi)/5)` and `cos((8pi)/5)+sin((8pi)/5)`

and these five roots, when graphed on the complex plane, are equally spaced around a circle of unit radius as shown below.

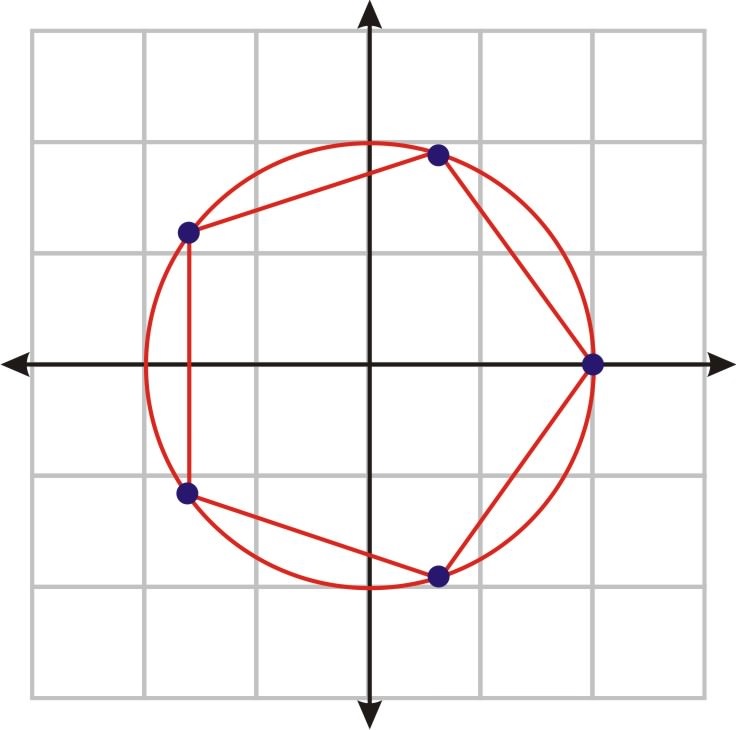
and it is apparent that their sum will be zero.

As such comparing real and imaginary parts we should have

`1+cos((2pi)/5)+cos((4pi)/5)+cos((6pi)/5)+cos((8pi)/5)=0`

and `0+sin((2pi)/5)+sin((4pi)/5)+sin((6pi)/5)+sin((8pi)/5)=0`

i.e. `cos((2pi)/5)+cos((4pi)/5)+cos((6pi)/5)+cos((8pi)/5)=-1`

and `sin((2pi)/5)+sin((4pi)/5)+sin((6pi)/5)+sin((8pi)/5)=0`