A disk has a mass 3.5 kg and radius 15 cm, rotating with angular speed 15 rev/s when a second disk of 5.0 kg is dropped onto it. If second disk has diameter 18 cm and mass 5.0 kg, what is the common final angular speed of the system?
1 Answer
Explanation:
Law of Conservation of angular momentum states:
The total angular momentum of a system about an axis remains constant, when the net external torque acting on the system about the given axis is zero.
This is applicable in the given question as a stationary second disk is dropped on a rotating disk. It is assumed that second disk is also mounted on the same shaft.
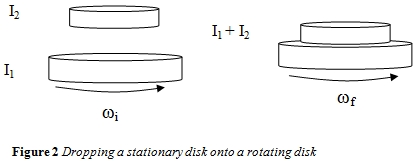
Angular momentum
where angular velocity of disk rotating with angular speed
Moment of inertia of disk
Initial Angular momentum
If
Final Angular momentum
Inserting given values and equating scalar part with (1) we get, (remember to change the given diameter of second disk to its radius)
