Find the points at which the tangent is horizontal? y = (cos(x))/(2 + sin(x))
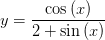
1 Answer
Considering trig functions are periodic, the tangents will be horizontal at
#x = pi/6 + 2pin# , n an integer
#x = (5pi)/6 + 2pin# , n an integer
Explanation:
We start by finding the derivative using the quotient rule.
#y' = (-sinx(2 + sinx) - cosx(cosx))/(2 + sinx)^2#
#y' = (-2sinx - sin^2x - cos^2x)/(2 + sinx)^2#
#y' = (-(2sinx + sin^2x + cos^2x))/(2 + sinx)^2#
#y' = - (1 - 2sinx)/(2 + sinx)^2#
Recall that the derivative represents the instantaneous rate of change of the function at any given point in its domain. Also recall that a horizontal line (e.g.
Set the derivative to
#0 = - (1 - 2sinx)/(2 + sinx)^2#
#0(2 + sinx)^2 = -(1 - 2sinx)#
#0 = 2sinx - 1#
#sinx = 1/2#
#x = pi/6 + 2pin, (5pi)/6 + 2pin#
Hopefully this helps!

