Question

If g(x)=x if x<0, x^2 if `0<= x <=1`, x^3 if x>1, how do you show that g is continuous on (all real #'s)?

Answer 1

The function `g(x)` is defined as follows `AA x in RR`:

`g(x) = { (x,x<0), (x^2, 0 le x le 1), (x^3, x > 1) :}`

Which we can graph as follows:

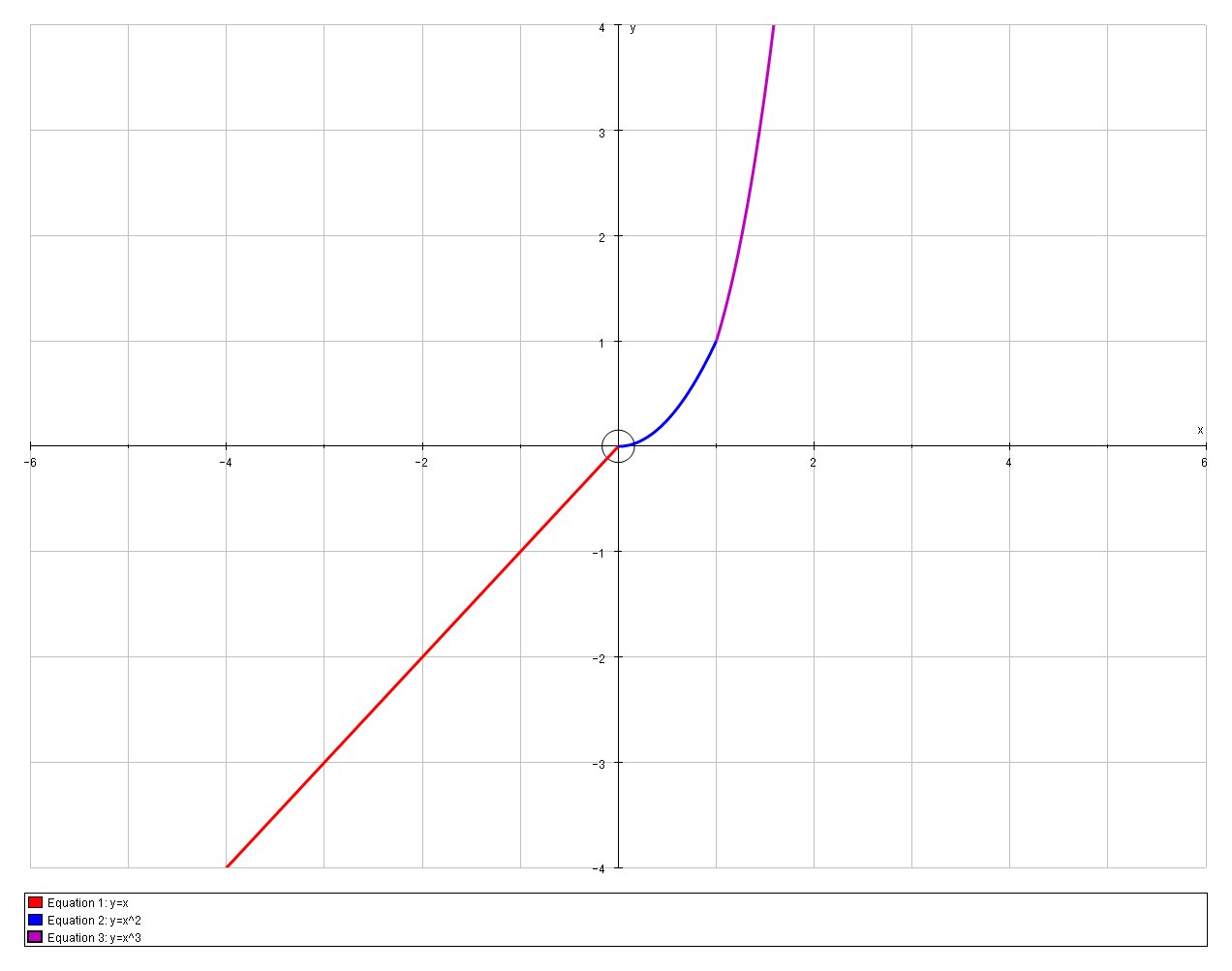
The individual functions `y=x, x^2` and `x^3` (being polynomials) are all continuous. In order to prove that `g(x)` is continuous we need to establish continuity at the connection points between the various curve segments, ie at `x=0` and `x=1`.

When `x=0`

Consider the left-hand limit:

`lim_(x rarr 0^-) g(x) = lim_(x rarr 0) x \ \= 0`

And the right-hand limit

`lim_(x rarr 0^+) g(x) = lim_(x rarr 0) x^2 = 0`

And the value of the function:

`g(0) = 0`

So `g(x)` is continuous at `x=0`

When `x=1`

Consider the left-hand limit:

`lim_(x rarr 1^-) g(x) = lim_(x rarr 1) x^2 \ \= 1`

And the right-hand limit

`lim_(x rarr 1^+) g(x) = lim_(x rarr 1) x^3 = 1`

And the value of the function:

`g(1) = 1`

So `g(x)` is continuous at `x=1`

Hence `g(x)` is continuous `AA x in RR`