If IA+BI = IA-BI, find the angle between the vector A and B and show that the two vectos are perpendicular to each other. How to answer this question?
3 Answers
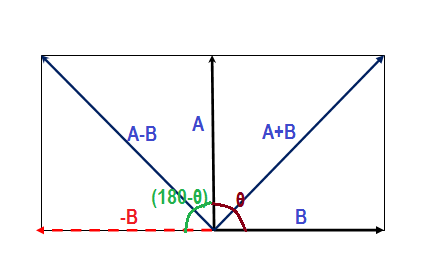
Let the angle between two vectors
So
Again
By the given condition
So
See below.
Explanation:
Considering that
If
or simplifying
This means that the scalar product of
We can use some properties of the Vector Norm.
# ||A|| = sqrt(A * A) => ||A||^2 = A * A #
We are given that:
# || A+B || = || A - B|| #
If we square both sides we get:
# || A+B ||^2 = || A - B||^2 #
Using the above property this becomes:
# (A+B) * (A+B) = (A - B) * (A-B) #
And the Vector Dot Product is distributive over vector addition so we can expand the above expression;
# (A+B) * A + (A+B) * B = (A - B) * A - (A - B) * B #
# :. A*A+B*A + A*B+B* B = A*A - B* A - A*B + B * B #
# :. B*A + A*B = - B* A - A*B #
And the vector product is Commutative so
# :. A*B + A*B = - A* B - A*B #
# :. 2A*B = -2 A* B #
# :. 4A*B = 0 #
# :. A*B = 0 #
And If
#A=0# or#B=0# ; or
#A# and#B# are perpendicular. QED



