Question

For the circle `(x+3)^2+(y-2)^2=10`, how do you find the equation of the tangent line at the point (-2,5)?

Answer 1

`y(x) = (13-x)/3`

Explanation:

We can evaluate the derivative `dy/dx` using implicit differentiation:

`(x+3)^2+(y-2)^2 = 10`

`d/dx(( x+3)^2+(y-2)^2 ) = 0`

`2(x+3) +2(y-2)dy/dx = 0`

`dy/dx = -(x+3)/(y-2)`

In the point `(-2,5)` the value of the derivative is then:

`[dy/dx]_(P=(-2,5)) = - (-2+3)/(5-2) = -1/3`

The equation of the tangent line is than:

`y(x) = y_0+y'(x_0)(x-x_0)`

that is:

`y(x) = 5-1/3(x+2)`

`y(x) = -1/3x+13/3`

`y(x) = (13-x)/3`

Answer 2

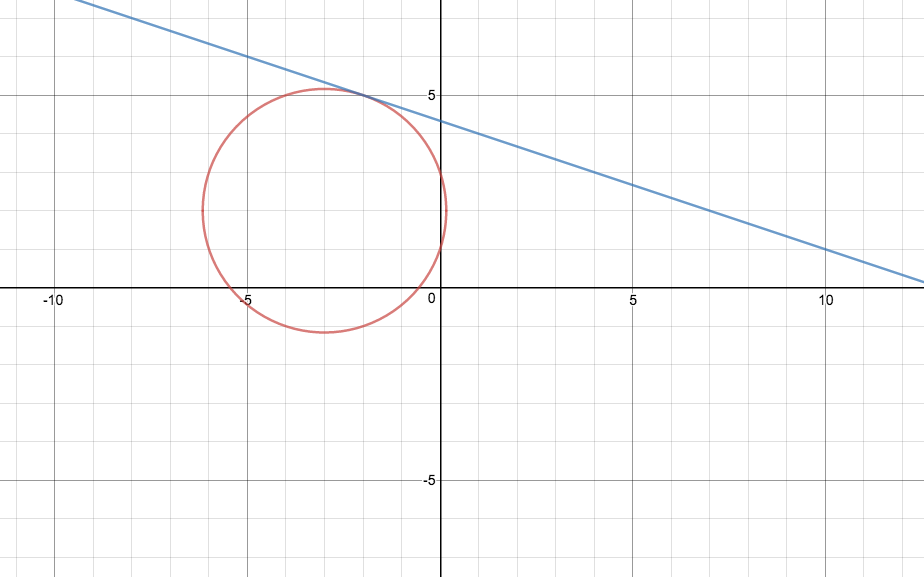
`y = -1/3x+13/3`

Explanation:

Another approach is using the properties of circles. We have

`(x+3)^2+(y-2)^2=10`

Which represents a circle of centre `(-3,2)` and radius `sqrt(5)`

First, let us very quickly verify `(-2,5)` lies on the circle:

`(x+3)^2+(y-2)^2=1^2+3^2=10`, which is good!

So the line passing through through `(-2,5)` and the centre `(-3,2)` will be perpendicular to the tangent (ie it will be the normal):

`m_N = (Delta y)/(Delta x) = (5-2)/(-2-(-3)) = 3`

As this perpendicular to the tangent the product of their gradients is `-1`; so

`m_T = -1/3`

So the tangent passes through `(-2,5)` and has gradient `m_T = -1/3` so using the point-slope formula fro a straight line, `y-y_1=m(x-x_1)`, the required equation is given by:

`\ \ \ \ \ y-5 = -1/3(x+2)`
`:. y-5 = -1/3x-2/3`
`:. \ \ \ \ \ \ y = -1/3x+13/3`