Question

Estimate the area under the curve `1/(x-1)^2` over the interval `[2,3]` with `n=4` using the trapezium rule?

Answer 1

Trapezium rule gives:

`int_2^3 \ 1/(x-1)^2 \ dx ~~ 0.51` (2dp)

Explanation:

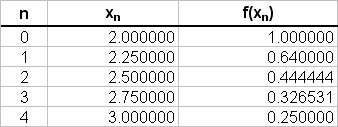
The values of `f(x)=1/(x-1)^2` are tabulated as follows (using Excel) working to 5dp

Using the trapezoidal rule:

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

We have:

`int_2^3 \ 1/(x-1)^2 \ dx`
`" " ~~ 0.25/2 { (1 + 0.25) + 2(0.64 + 0.444444 + 0.32653) }`
`" " = 0.125 { 1.25 + 2(1.410975) }`
`" " = 0.125 { 1.25 + 2.82195 }`
`" " = 0.125 { 4.07195 }`
`" " = 0.508993`

Let's compare this to the exact value:

`int_2^3 \ 1/(x-1)^2 \ dx = [-1/(x-1)]_2^3`
`" " = -(1/2-1)`
`" " = 0.5`