The first quadrant region enclosed by y=2x, the x-axis and the line x=1 is resolved about the line y=0. How do you find the resulting volume?
1 Answer
Evaluate
Explanation:
The region is shown in the graph below.
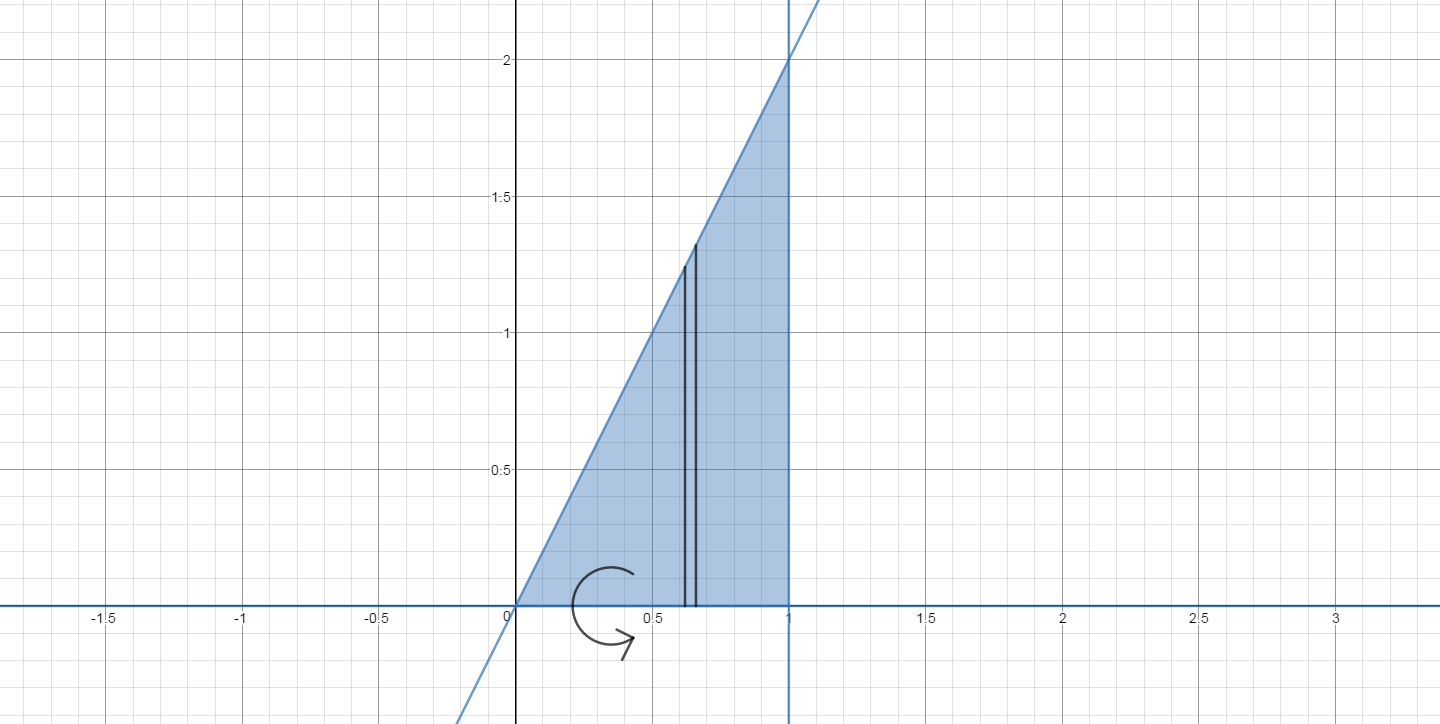
The graph shows a representative slice of the region. The slice is taken at some value of
When rotated about the
The volume of the representative disk is
In this case we have:
the volume of the slice is
Note
Because the question was posted under the topic "Calculating Volumes using Integrals", I have used the integral.
With some imagination we might notice that the solid will be a right circular cone.
The cone will have radius
The volume of a right circular cone is
Using this formula we also get

