How do you find the equation of the line tangent to #y = x^(3) + 2x^(2) - 3x + 2# at the point where x = 1?
2 Answers
The tangent line is:
Explanation:
For
so the curve goes through the point:
The equation of the tangent line is then:
where:
and:
So the tangent line is:
or:
Explanation:
The point on the graph of
Since the only things we need to know to write the equation of the line are a point it travels through and its slope, we just need to know the slope of the tangent line at
Luckily for this, this is exactly what the derivative of the function tells us. The derivative, evaluated at
To find the derivative of
Also remember that constants don't really matter when we're finding the derivative of something--they stay when we differentiate a function. So, where
So, when we take the derivative of
Note that
Then:
So the value of the derivative
So we know the tangent line has slope
The equation for a line passing through
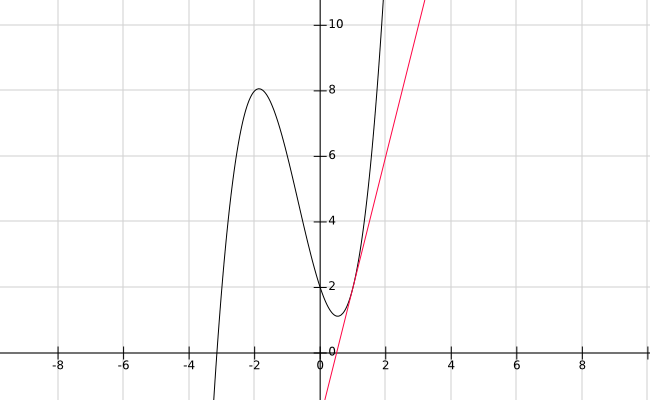
Graphed are the original function and its tangent line at
graph{(-y+x^3+2x^2-3x+2)(y-4x+2)=0 [-5, 5, -8, 15.26]}


