Question

The terminal side of `theta` lies on the line `2x-y=0` in quadrant III, how do you find the values of the six trigonometric functions by finding a point on the line?

Answer 1

#{:(sin(theta)=-2/sqrt(3),color(white)("XX"),csc(theta)=-sqrt(3)/2), (cos(theta)=-1/sqrt(3),,sec(theta)=-sqrt(3)), (tan(theta)=2,,cot(theta)=1/2) :}#

Explanation:

Any relation of the form `Ax+By=C` has a slope of (i.e. a `tan`) `-A/B`
So `2x-y=0` has a slope (`tan`) of `2`.

Furthermore, we can see that `2x-y=0` passes through the origin,
so we have the situation in the image below for a point on the line in Q III:

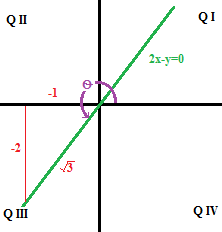
The six trigonometric values can be determined by applying their definitions based on "adjacent", "opposite", and "hypotenuse" sides.

Answer 2

The answer is:
`sin theta = -(2sqrt(5))/5`

`cos theta = - sqrt(5)/5`

Because `sqrt(2^2 + (-1)^2) = sqrt(5)`

Explanation:

Using the distance formula you arrive at the square root of 5. This answer is verified via a Larson Precalculus book in the answer section.

EDIT: How I did this was by picking a relivant point that I could work with. You could also use the unit circle equation of `x^2 + y^2 = 1` to find the answer as well. With 2x - y = 0 moving the y to the right you end up with 2x = y (y = 2x). your unit circle equation becomes `x^2 + (2x)^2 = 1` and you solve from there to end up with the answers above.