How to long divide #(x^3-2x^2-4x-4)/(x^2+x-2)#?
1 Answer
Apr 16, 2017
Explanation:
By long division,
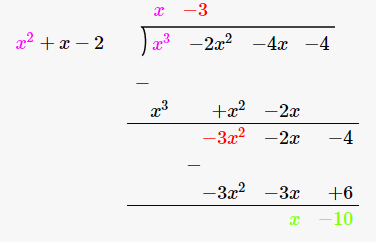
Hence,
Then, let
Multiply throughout by
When
When
Hence, substitute
By long division,
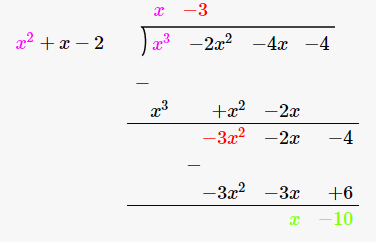
Hence,
Then, let
Multiply throughout by
When
When
Hence, substitute