Question

What is the general rule for a line on a 3D plane and what should you use for m instead of rise/run?

I know the general rule for a line on a 2D plane is `y=mx+c`, but what is the general rule for a line on a 3D plane? Does it somehow use rise, run and tilt (z axis) in m? Does it still only use the y intercept or does it need others as well?

Answer 1

I tried this hoping not to confuse you too much!

Explanation:

A line in 3D is represented through the junction of two planes ! Consider taking two sheets of paper; cut a small line into both and insert one into the other...you'll get a line as the intersection:

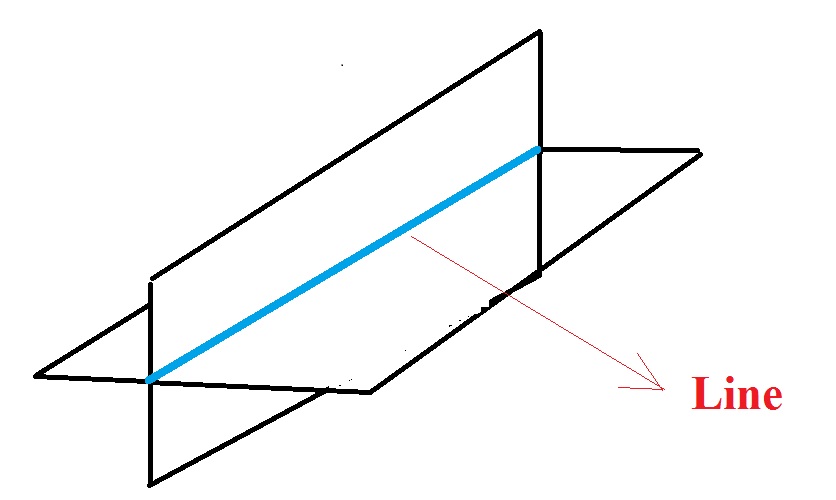
So instead of having one equation, in 3D, you'll need two equations each one representing a plane and forming a System such as:
`{(ax+by+cz=d),(ex+fy+gz=k):}`

For the slope can consider the PROJECTIONS of your line and the components on each axis:

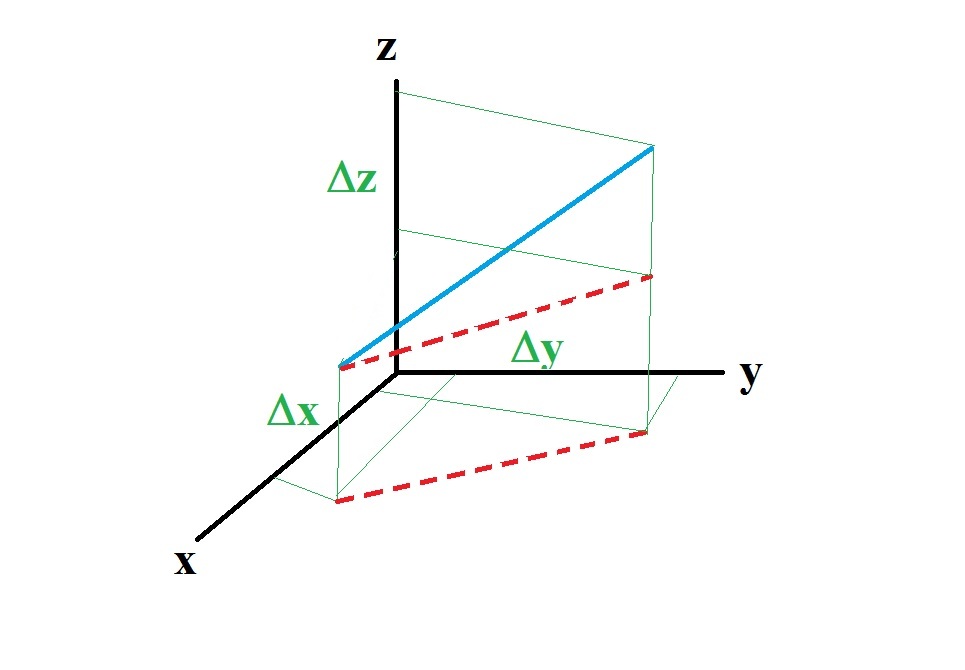
Although my drawing is not really good we can see that:
`"slope"="rise"/"run"=(Deltaz)/(sqrt((Deltax)^2+(Deltay)^2))`
where the denominator is our good old Pythagoras Theorem.